Dimensionnement d’un gratte-ciel et étude des possibilités de raidissement d’une construction en hauteur

1.2 Couplage de refends

La différence entre ce système et le précédent est l’interconnexion des murs par des poutres ou des dalles très rigides de manière à ce qu’ils travaillent ensemble. La rigidité totale du système est alors supérieure à la somme des rigidités individuelles

des refends. Ce système, composé de refends fonctionnant comme des porte-à-faux, peut être utilisé pour résister à des charges horizontales jusqu’à une hauteur d’environ 25 étages.
Ces refends ainsi couplés auront fréquemment une forme de L ou U constante sur la hauteur, car cela permet d’y insérer tous les cheminements verticaux (escaliers, ascenseurs, conduits,…). Contrairement à un simple mur, rigide dans une seule direction, ce couplage les rend efficaces dans les deux directions principales.

1.3 Cadres rigides

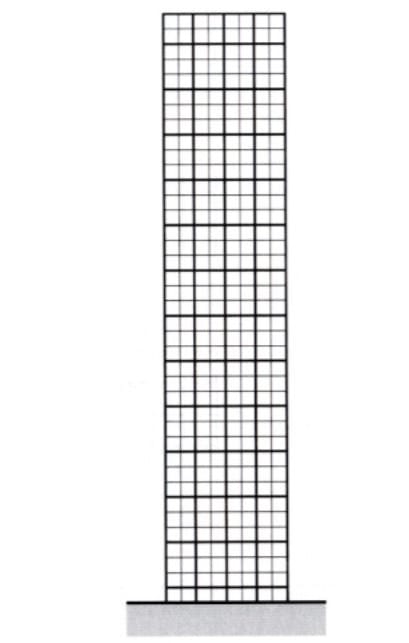
Ce système se compose de colonnes et de dalles rigidement liées. Les dalles peuvent être assimilées à des poutres si leur épaisseur est suffisante ou si elles sont composées de sommiers reliant directement deux colonnes. Le système ainsi composé se comporte comme un cadre permettant de reprendre aussi bien un effort tranchant qu’un moment de flexion.

Ce genre de système est adapté pour des structures jusqu’à 25-30 étages. Coulé en place, le béton présente donc l’avantage de créer des joints continus. Néanmoins, une attention particulière devra être portée à la conception des détails afin d’assurer la rigidité de la liaison au niveau des armatures.

Dans les bâtiments à étages multiples, des ouvertures centrales permettant les circulations verticales sont toujours construites. Ces ouvertures sont souvent utilisées pour des cages d’ascenseur ou d’escaliers ne nécessitant généralement pas de lumière naturelle. Il est donc très fréquent de les construire en béton armé, ce qui crée une structure verticale très rigide appelée : « noyau ». Souvent situé dans la partie centrale de la construction, ce noyau travaille comme une poutre console encastrée dans les fondations.

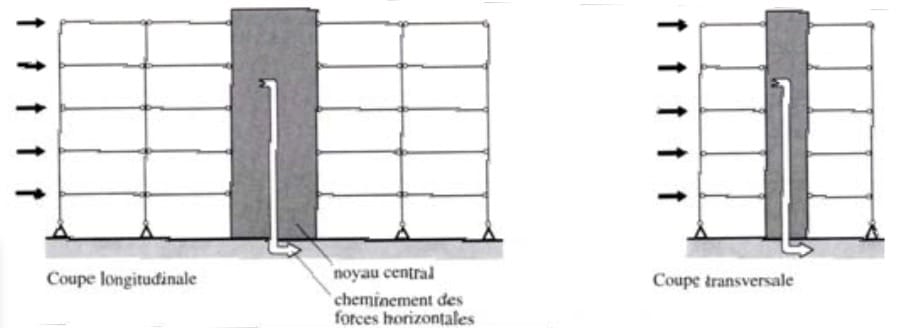
L’avantage principal de ces structures est la forme du noyau leur permettant de résister à tous types de charges : verticales, efforts tranchants, moments de flexion dans les deux directions et torsion. Il reprend donc la majorité des forces horizontales qui lui sont transmises par l’intermédiaire des dalles jusqu’à environ 40 étages.

Il faudra, pour ces structures, faire attention aux effets différés du béton, et ce particulièrement si le reste de la structure est en acier.

1.5 Interaction murs/noyau(x) et cadres

Ce système est sans conteste le plus utilisé pour la construction de systèmes résistants aux charges latérales. Il peut aussi bien être appliqué pour des bâtiments de 10 étages que pour des gratte-ciel jusqu’à 50 étages.

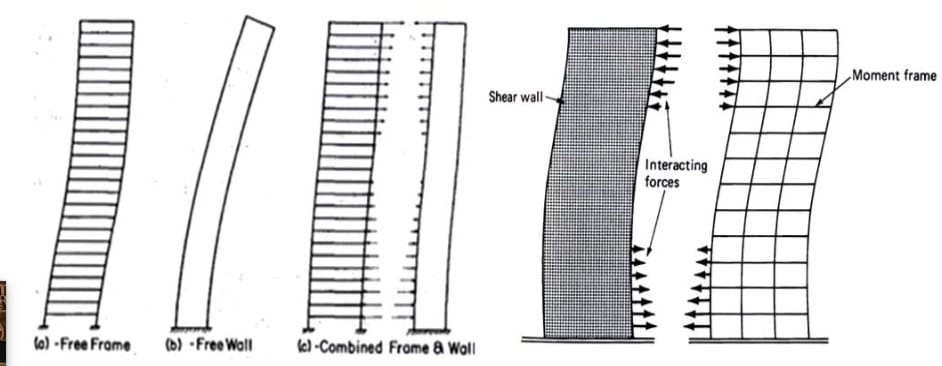
L’interaction des cadres (dalles + montants) et des murs ou noyau(x) a été comprise il y a déjà longtemps. Le mode d’interaction classique entre les deux systèmes est illustré à la Figure 5 ci-dessous. Les cadres se déforment principalement au cisaillement tandis que le(s) noyau(x) et les murs répondent, comme des poutres consoles, avec une déformation à la flexion. La compatibilité des déformations horizontales produit alors une interaction entre les deux systèmes. La forme linéaire du diagramme des moments des cadres, combinée avec la forme parabolique de celui du noyau produisent des déformations qui engendrent une rigidité accrue du système. Le noyau est retenu dans la partie haute de la construction de même que les cadres en partie basse.

Le(s) étage(s) de raidissement sont des étages très rigides, sur un ou plusieurs niveaux, composés essentiellement de murs reliant le noyau aux colonnes. Cette liaison ainsi créée permet de rigidifier la structure en faisant participer les montants à la reprise des moments de flexion. Le système est alors composé d’une poutre console encastrée dans les fondations (noyau) et de tirants/butons (montants) reliés

au noyau par une traverse très rigide. Il est également possible de trouver des étages de raidissement composés de treillis horizontaux. Dans le cas ou un seul étage de raidissement est disposé, il est possible de déterminer sa position optimale vis-à-vis des déplacements horizontaux au sommet.

Ce calcul est réalisé au §3.3.3 et indique que cette position est à z H = 0.54 mesurée
depuis la base du gratte ciel.

Au sommaire

0 Introduction

1 Principaux systèmes structuraux de raidissement

• 1.1 Dalles sur murs et/ou colonnes
• 1.2 Couplage de refends
• 1.3 Cadres rigides
• 1.4 Noyau(x)
• 1.5 Interaction murs/noyau(x) et cadres
• 1.6 Noyau(x) et étage(s) de raidissement
• 1.7 Divers systèmes composites
• 1.8 Systèmes tube

2 Structure du gratte-ciel

• 2.1 Structure adaptée pour ce projet
• 2.1.1 Description de la construction
• 2.1.2 Utilisation prévue
• 2.1.3 Durée de service prévue
• 2.1.4 Durabilité de l’ouvrage
• 2.1.5 Système structural
• 2.1.6 Données géométriques principales
• 2.1.7 Matériaux de construction
• 2.1.8 Détails de construction
• 2.1.9 Procédé d’exécution
• 2.2 Principales modifications
• 2.3 Dimensions et matériaux utilisés
• 2.4 Système de raidissement du gratte-ciel

3 Optimisation du système de raidissement du gratte-ciel

• 3.1 Modèle théorique de comportement
• 3.1.1 Bases théoriques
• 3.1.2 Modèle mathématique
• 3.2 Paramètres du modèle
• 3.2.1 Inertie du noyau
• 3.2.2 Rigidité latérale des cadres (GA*)
• 3.2.3 Charges de vent
• 3.3 Résolutions théoriques
• 3.3.1 Résolution de l’équation différentielle de comportement
• 3.3.2 Noyau seul
• 3.3.3 Noyau – étage de raidissement (EI∞ et rotation bloquée)

• 3.3.4 Noyau – cadres
• 3.3.5 Noyau – cadres – étage raidissement (EI∞ et rotation bloquée)
• 3.3.6 Noyau – étage de raidissement (EI∞ et rotation admise)
• 3.3.7 Noyau – étage de raidissement (EIr et rotation admise)
• 3.3.8 Synthèse des résultats
• 3.4 Résolution méthode « Khan & Sbarounis »
• 3.4.1 Concept et méthode d’analyse
• 3.4.2 Méthode de calcul
• 3.4.3 Résultats
• 3.5 Résolution matricielle (nœuds par nœuds)
• 3.5.1 Système simplifié
• 3.5.2 Résultats
• 3.6 Résolutions systèmes numériques 2D
• 3.6.1 Modélisations numériques 2D
• 3.6.2 Rigidité EI équivalente, système W
• 3.6.3 Rigidité GA* équivalente, système F
• 3.6.4 Variantes de calcul
• 3.6.5 Noyau seul
• 3.6.6 Noyau – étage de raidissement (EI∞ et rotation bloquée)
• 3.6.7 Noyau – cadres
• 3.6.8 Noyau – cadres – étage raidissement (EI∞ et rotation bloquée)
• 3.6.9 Noyau – étage de raidissement (EI∞ et rotation admise)
• 3.6.10 Noyau – étage de raidissement (EIr et rotation admise)
• 3.6.11 Synthèse des résultats
• 3.7 Résolutions systèmes numériques 3D
• 3.7.1 Colonnes
• 3.7.2 Noyau
• 3.7.3 Dalles
• 3.7.4 Appuis
• 3.7.5 Étage de raidissement
• 3.7.6 Charges de vent
• 3.7.7 Maillage
• 3.7.8 Modélisation complète
• 3.7.9 Résolutions numériques 3D, dalles 300[mm]
• 3.7.10 Résolutions numériques 3D, dalles 10[mm]
• 3.7.11 Synthèse des résultats
• 3.8 Comparaison des modèles et influence des différents paramètres
• 3.8.1 Comparaisons entre résolutions théoriques
• 3.8.2 Comparaisons entre résolutions théoriques et numériques 2D
• 3.8.3 Comparaisons entre résolutions numériques 2D
• 3.8.4 Comparaison finale avec les résolutions numériques 3D

• 3.9 Position optimale de l’étage de raidissement
• 3.9.1 Paramètres non considérés
• 3.9.2 Position optimale vis-à-vis des déplacements sommitaux
• 3.9.3 Autres critères d’optimisation
• 3.9.4 Position retenue dans le cadre d’un projet réel
• 3.10 Questions générales
• 3.10.1 Règle empirique de la position optimale à 2/3H
• 3.10.2 Position sommitale de l’étage de raidissement dans le projet réel à Madrid

4 Redistribution des efforts, effets différés différentiels

• 4.1 Problématique
• 4.2 Modèle théorique de comportement
• 4.2.1 Déformation instantanée
• 4.2.2 Déformation de retrait
• 4.2.3 Déformation de fluage
• 4.2.4 Principe de superposition
• 4.3 Analyse des effets différés
• 4.3.1 Équation intégrale de Volterra
• 4.3.2 Méthode du coefficient de vieillissement
• 4.3.3 Redistribution des efforts dans les éléments verticaux
• 4.3.4 Facteur de correction dû aux barres d’armature
• 4.4 Descente de charges
• 4.5 Retrait
• 4.5.1 Situation de charge déterminante
• 4.5.2 Déformations différées de retrait
• 4.5.3 Redistribution des efforts due aux déformations différentielles de retrait
• 4.6 Fluage
• 4.6.1 Hypothèses de calcul
• 4.6.2 Déformations différées de fluage
• 4.6.3 Redistribution des efforts due aux déformations différentielles de fluage
• 4.7 Synthèse effets différés

5 Conclusion

6 Bibliographie

• 6.1 Livres, polycopiés, publications
• 6.2 Articles
• 6.3 Notes de cours
• 6.4 Sites Web