10,K
Dimensionnement des structures
Une structure est un assemblage intelligent d’éléments et de matériaux afin d’assurer une fonction.
La figure I.1 montre par exemple la structure en balsa d’un avion d’aéromodélisme permettant d’assurer la forme de la voilure portante, ainsi que la structure d’un pylône électrique qui permet de maintenir les lignes électriques à une certaine hauteur.
Le but du dimensionnement est de déterminer les formes, dimensions, matériaux afin de satisfaire la fonction demandée dans toutes les conditions de vie de la structure. Par exemple la structure en balsa de l’avion d’aéromodélisme doit résister aux efforts aérodynamiques
Figure I.1 – Exemples de structures : structure en balsa d’un avion d’aéromodélisme, pylône électrique
Figure I.2 – Problème réel : dimensionnement des pieds d’une table.
en vol, la structure du pylône électrique doit résister à des vents forts et des surcharges de neige et de verglas.
Deux principales méthodes existent pour dimensionner une structure :
- Méthode non prédictive « essai-erreur » : on construit un prototype réel (ou une maquette à échelle réduite), puis on le teste en condition réelle ; cette méthode a l’avantage de ne faire appel à aucune connaissance a priori de la mécanique mais est coûteuse.
- Méthode prédictive : on fait un modèle mécanique « virtuel » basé sur des équations mathématiques, puis on le teste ; cette méthode est moins coûteuse, mais a l’inconvénient de faire appel à des connaissances de mécanique et de mathématiques.
C’est cette deuxième méthode qui est développée dans ce cours. On se limite au dimensionnement des structures en statique et en élasticité linéaire.
Problème réel
Le problème réel fait intervenir (Fig. I.2) :
- Une structure, comprenant des incertitudes sur sa géométrie et son matériau ;
- Des liaisons avec l’extérieur, souvent assez mal maîtrisées ;
- Des efforts appliqués, parfois assez complexes.
Lors de la phase de conception, la solution réelle de ce problème n’est pas accessible (déplacements, contraintes, …). Une fois la structure fabriquée et placée dans son environnement, la solution est partiellement accessible par des mesures (jauges de déformation, photoélasticité,… ).
I.1.1 Modéle mécanique
Afin de trouver une solution approchée du problème réel, on utilise un modèle mathématique du problème réel. Les modèles généralement utilisés en mécanique sont :
- le modèle de poutre,
- le modèle de plaque,
- le modèle de coque,
- le modèle plan en contraintes planes,
- le modèle plan en déformations planes,
- le modèle axisymétrique,
- le modèle tri-dimensionnel.
Pour l’exemple précédent d’un pied de table, on peut par exemple choisir :
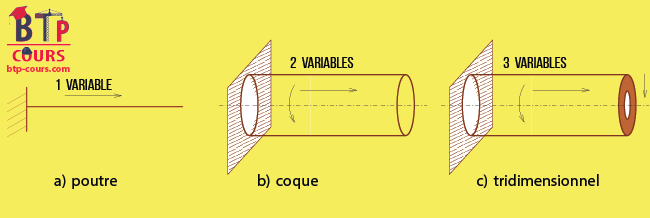
- Le modèle de poutre (Fig. I.3 a) :
- hypothèse cinématique de poutre
- 1 variable le long de l’axe de la poutre décrit le problème
- encastrement de type poutre
- torseurs d’efforts équivalents
- Le modèle de coque (Fig. I.3 b) :
- hypothèse cinématique de coque
- 2 variables sur la surface moyenne de la coque décrivent le problème
- encastrement de type coque
- torseurs d’efforts équivalents distribués
- Le modèle tri-dimensionnel (Fig. I.3 c) :
- encastrement tri-dimensionnel
- 3 variables dans les 3 directions de l’espace décrivent le problème
- forces surfaciques distribuées
Pour les trois modèles proposés, l’encastrement est modélisé de façon parfaite alors que la liaison réelle est réalisée par une pièce intermédiaire souple. Ces modèles ne permettent pas de dimensionner cette pièce intermédiaire. C’est au concepteur de choisir le modèle le plus adapté par rapport aux critères de dimensionnement qu’il pense être les plus judicieux.
Au sommaire:
I – Poutre et torseur de cohésion
- I.1 Introduction au dimensionnement des structures
- I.1.1 Modéle mécanique
- I.2 Modèle de poutre
- I.3 Poutre dans son environnement
- I.4 Torseur de cohésion
- I.4.1 Définition
- I.4.2 Détermination
- I.4.3 Classification des sollicitations
II – Sollicitations simples sur les poutres
- II.1 Traction
- II.1.1 Torseur de cohésion
- II.1.2 Contrainte normale
- II.1.3 Allongement, déformation et déplacement
- II.1.4 Relation contrainte-déformation
- II.1.5 Relation entre effort normal et chargement
- II.2 Torsion
- II.2.1 Torseur de cohésion
- II.2.2 Moment quadratique polaire de section
- II.2.3 Contrainte tangentielle
- II.2.4 Déformation et rotation des sections
- II.2.5 Relation contrainte-déformation
- II.2.6 Relation entre moment de torsion et chargement
- II.3 Flexion
- II.3.1 Torseur de cohésion
- II.3.2 Moment quadratique de section
- II.3.3 Contrainte normale
- II.3.4 Déformation
- II.3.5 Déplacement
- II.3.6 Relation contrainte-déformation
- II.3.7 Relations moment de flexion – effort tranchant – chargement
III – Calcul de treillis
- III.1 Hypothèses et critère de dimensionnement
- III.1.1 Hypothèses sur les liaisons
- III.1.2 Règles de construction d’un treillis
- III.1.3 Critère de dimensionnement
- III.2 Méthode des nœuds
- III.3 Flambage des poutres droites
- III.3.1 Introduction
- III.3.2 Charge critique de flambage d’une poutre droite
- III.3.3 Élancement et rayon de giration
- III.3.4 Critère de dimensionnement
- III.3.5 Autres conditions aux limites
IV – Contraintes et déformations
- IV.1 Introduction
- IV.2 Caractérisation des contraintes et des déformations tridimensionnelles
- IV.2.1 Opérateur des contraintes et des déformations
- IV.2.2 Théorème de superposition
- IV.3 Problème plan
- IV.3.1 Hypothèses
- IV.3.2 Etat de contraintes planes
- IV.3.3 Expressions des contraintes subies par un carré non aligné avec x et y
- IV.3.4 Expressions des déformations d’un carré non aligné avec x et y
- IV.3.5 Relation entre les contraintes et les déformations d’un carré non aligné avec x et y
- IV.3.6 Directions principales
- IV.3.7 Cercle de Mohr des contraintes
V – Critères de dimensionnement
- V.1 Objectifs
- V.2 Matériaux ductiles : critère de Tresca
- V.3 Matériaux ductiles : critère de Von Mises
- V.4 Comparaison des critères de Tresca et de Von Mises
- V.5 Fatigue des matériaux
VI – Enveloppes minces
- VI.1 Action d’un fluide au repos sur un solide
- VI.2 Application à un réservoir cylindrique
- VII Initiation au calcul éléments finis
- VII.1 Étude de l’élément de barre
- VII.1.1 Équilibre de l’élément barre
- VII.1.2 Exemple d’application
- VII.1.3 Remarques sur la méthode des éléments finis
- VII.2 Étude de deux barres
- VII.2.1 Assemblage des matrices de rigidité élémentaires
- VII.2.2 Mise en œuvre pratique
- VII.3 Élément barre pour le calcul des treillis
- VII.4 Élément de poutre pour le calcul des portiques
VIII – Moyens expérimentaux
- VIII.1 Jauges de déformation
- VIII.1.1 Principe
- VIII.1.2 Pont de Wheatstone
- VIII.1.3 Utilisation du boîtier
- VIII.1.4 Différents montages
- VIII.1.5 Capteurs à jauges
- VIII.1.6 Exploitation d’une rosette de 3 jauges à 45o
- VIII.2 Photoélasticité
- VIII.2.1 Principes
- VIII.2.2 Mise en équation
- VIII.2.3 Réseaux de courbes caractéristiques
Aperçu du document en ligne
Télécharger
Dimensionnement des structures
Mot clés: calcul de structure, Livre BTP, Livre Génie civil, Document BTP, Livre architecture, document génie civil, Dimensionnement des structures, calcul structure, calcul structure métallique, calcul des structures, calcul poutre, rdm




2 Commentaires
Merci beaucoup et qu'Allah vous récompense c'est bien ce que vous faites jaim
Kassoumcoulibaly28@yahoo.fr