Dessin: lecture de plans appliquée à l’installateur sanitaire

AVANT-PROPOS

L’élargissement du champ d’activités du Fonds de Formation professionnelle de la Construction au secteur du Parachèvement s’est accompagné d’un partage des responsabilités entre une série de groupes de travail : les «Sections FFC».

La section «Installations sanitaires, Matériaux synthétiques et Gaz» avait décidé, au départ, de réaliser un manuel scolaire. Au cours de l’évolution des travaux, ce manuel a pris plutôt la forme d’un ouvrage de référence pour la formation.

C’est ainsi qu’il ambitionne de toucher un public aussi large que possible : les élèves du secondaire, les adultes en formation, les formateurs et, en fi n de compte… les professionnels eux-mêmes.

Afin de faciliter la tâche du lecteur, nous avons subdivisé l’ouvrage en différentes brochures d’une quarantaine de pages chacune.

Une farde spéciale de classement est disponible pour les personnes qui désirent se procurer plu sieurs brochures ou la série complète. Vous trouverez une présentation de l’ensemble de la structure de l’ouvrage au verso de la page de couverture.

Nous espérons que cet ouvrage contribuera à rendre la formation plus homogène et sommes convain cus qu’il permettra tant aux élèves qu’aux adultes en formation de se familiariser agréablement avec les multiples facettes du métier d’installateur sanitaire.

Nous voudrions remercier ici tous les enseignants qui ont participé à la réalisation de ce travail de longue haleine ainsi que les fi rmes qui nous ont aidés à choisir les illustrations et à corriger certains textes.

Nous voudrions mentionner tout spécialement Messieurs N. De Pue (†) (ancien président de la F.B.I.C. – Fédération Nationale des Associations de Patrons Installateurs Sanitaires et de Chauffage au gaz, Plombiers, Zingueurs et Ardoisiers-Couvreurs de Belgique) et G. Wouters (président ho no rai re de la Verenigde Lood- en Zinkbewerkers, Antwerpen) qui ont contribué à ce projet et en ont rendu possible la réalisation.

Nous vous souhaitons beaucoup de plaisir dans votre lecture.

II.1. AVANT-PROPOS

Le module II “Dessin: lecture de plans“ analyse des exemples de constructions géométriques et explique la lecture d’un plan de construction.

Bien entendu, nous n’étudierons qu’un seul exemple tiré de la pratique journalière. Il faudra bien se rendre compte qu’une fois sur le chantier, une certaine souplesse sera nécessaire pour déchiffrer d’autres plans.

Le chapitre “Représentation des symboles sanitaires” sera également repris dans ce module car il constitue la base d’un plan sanitaire détaillé.

Le chapitre “Dessin fonctionnel sur ordinateur” s’appuie sur un programme moderne, choisi parmi les nombreux logiciels développés sur le marché. Le but de notre cours n’est, en effet, pas de maîtriser un tel logiciel, mais plutôt de comprendre la philosophie profonde du dessin par ordinateur.

II.2. DESSIN DE CONSTRUCTIONS GÉOMÉTRIQUES

En 3 couleurs: en noir: les lignes originales; en bleu: les lignes souhaitées et en rouge, les lignes auxiliaires

II.2.1. PERPENDICULAIRES

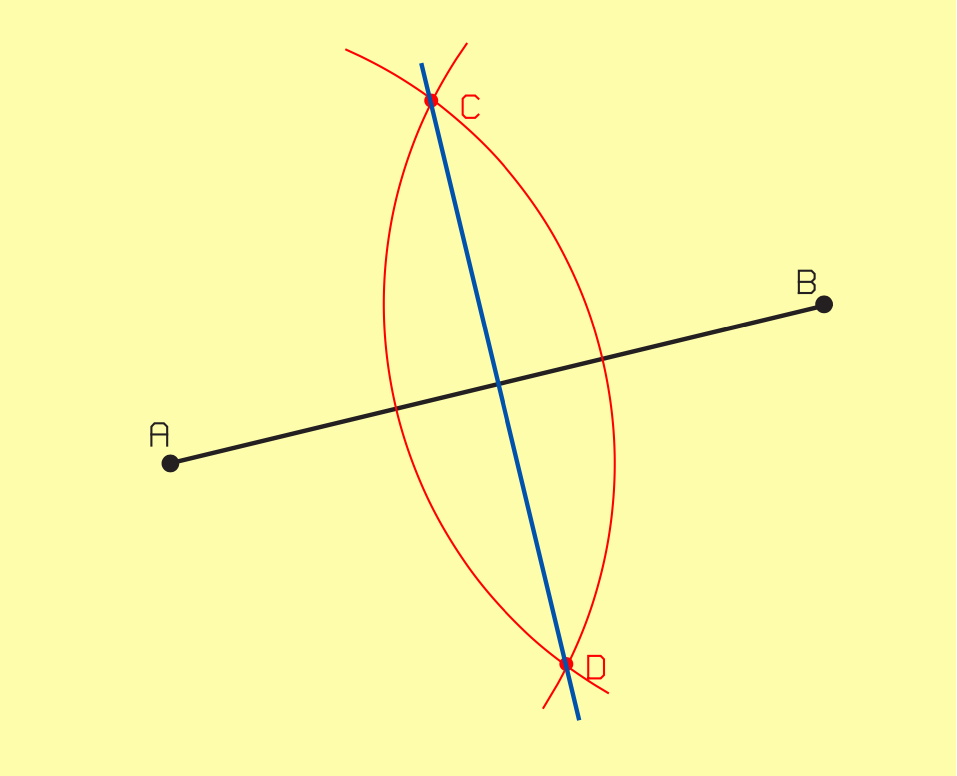
II.2.1.1. Perpendiculaire au milieu d’un segment de droite [AB]

1. À partir du point A, tracez un arc de cercle dont le rayon est supérieur à la moitié de AB.
2. À partir du point B, tracez un arc de cercle de rayon identique.
3. Reliez les points d’intersection C et D.

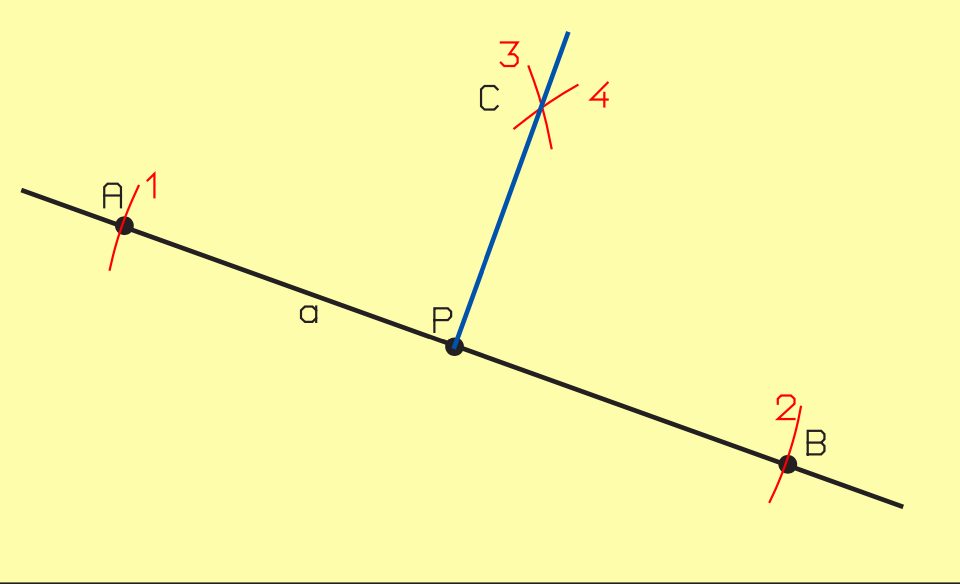
II.2.1.2. Perpendiculaire en un point donné d’une droite a

1. Tracez les arcs de cercle 1 et 2, de rayon quelconque, depuis le point P.
2. Tracez les arcs de cercle 3 et 4, de rayon supérieur à celui utilisé ci-dessus.
3. Tracez une ligne reliant P et le point d’intersection C.

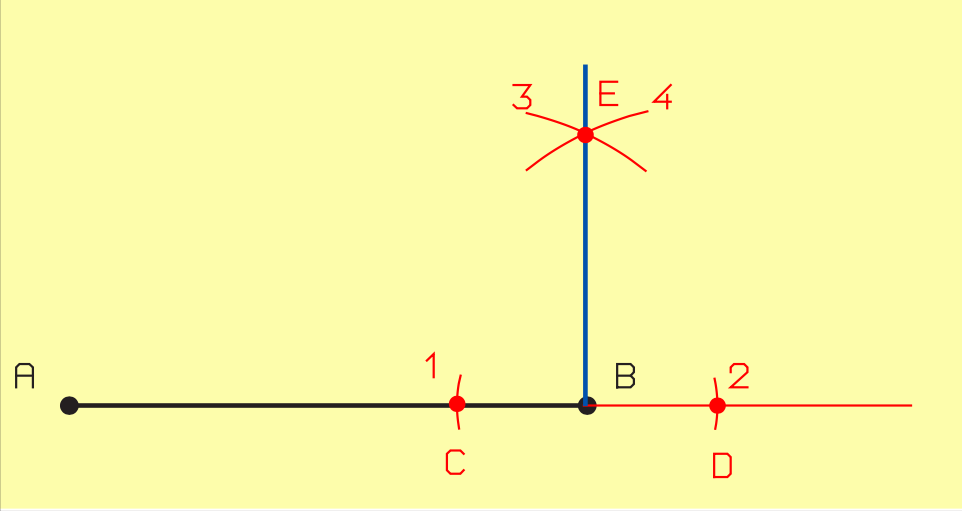
II.2.1.3. Perpendiculaire à l’extrémité d’un segment de droite [AB], méthode 1

1. Tracez l’arc 1, de rayon quelconque, depuis B.
2. Tracez l’arc 2, de même rayon, depuis C.
3. Tracez l’arc 3, de même rayon, depuis D.
4. Tracez une ligne auxiliaire entre les points d’intersection C et D.
5. Tracez maintenant la perpendiculaire reliant B et le point d’intersection E.

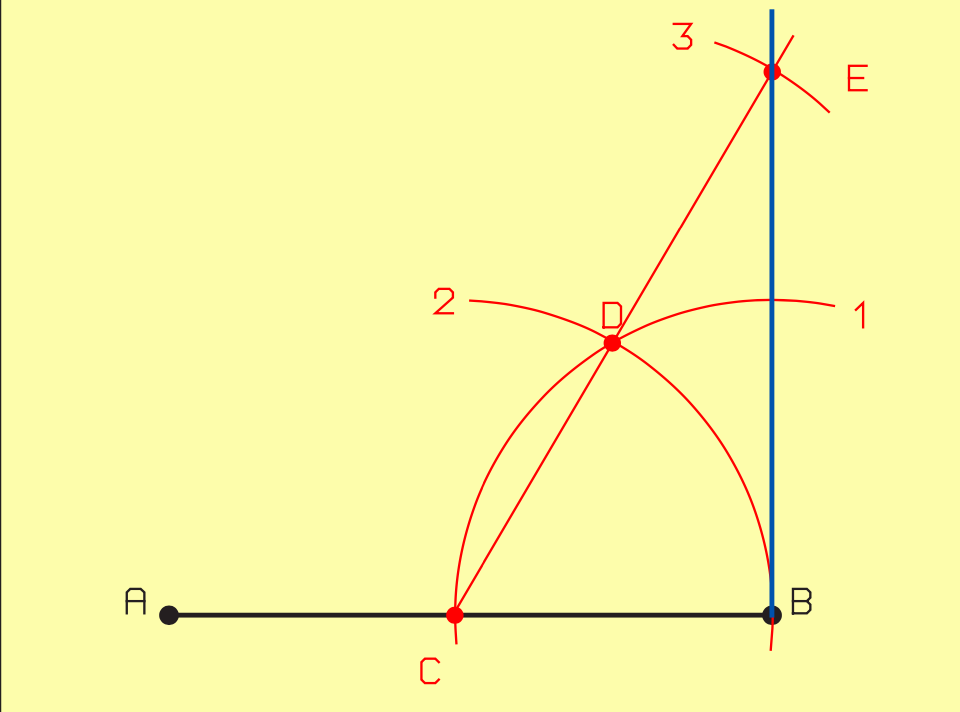
II.2.1.4. Perpendiculaire à l’extrémité d’un segment de droite [AB], méthode 2

1. Prolongez [AB] du côté où la perpendiculaire doit être élevée.
2. Tracez les arcs 1 et 2, de rayon quelconque, depuis B.
3. Tracez les arcs 3 et 4, de rayon supérieur à celui utilisé ci-dessus, à partir des points d’inter section C et D.
4. Tracez maintenant la perpendiculaire reliant B et le point d’intersection E.

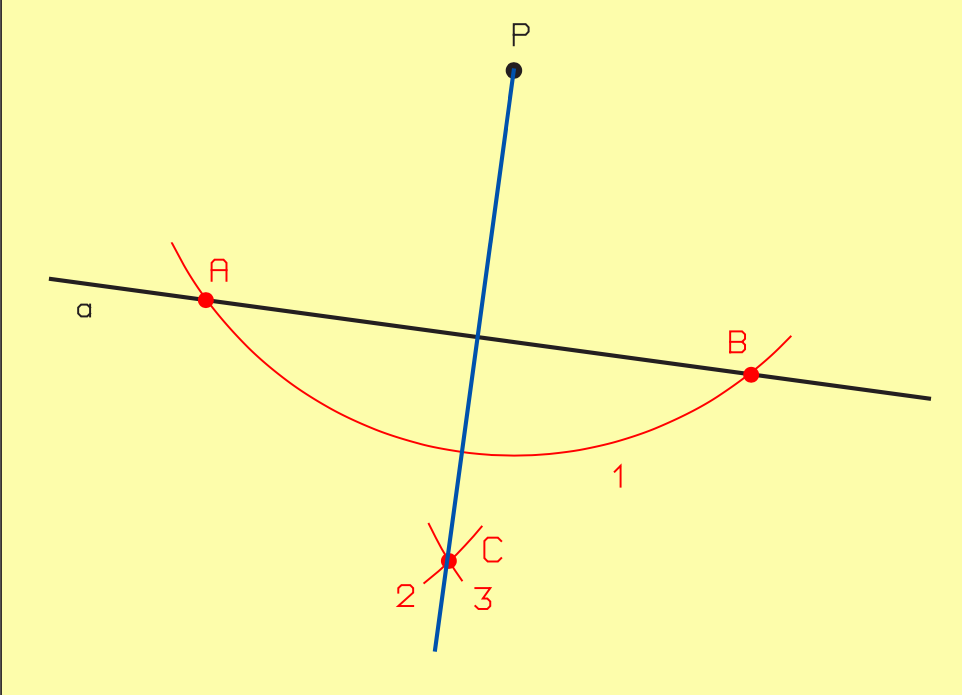
II.2.1.5. Perpendiculaire à une droite a à partir d’un point P

1. Depuis P, tracez l’arc 1, de rayon supérieur à la distance la plus courte entre P et la ligne a.
2. À partir de A, tracez l’arc 2, de rayon supérieur à la moitié de AB.
3. À partir de B, tracez l’arc 3, de rayon identique.
4. Tracez maintenant la perpendiculaire reliant P et le point d’intersection C.

II.2.2. PARALLÈLES

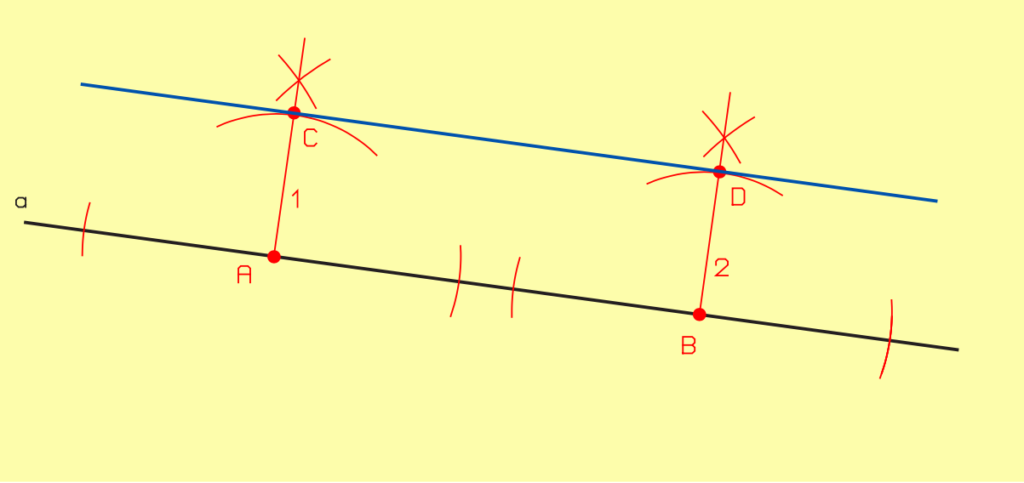
II.2.2.1. Parallèle à une distance donnée, par exemple 18 mm

1. À partir d’un point quelconque A, élevez la perpendiculaire (1).
2. À partir d’un point quelconque B, élevez la perpendiculaire (2).
3. À partir des points A et B, tracez un arc de 18 mm de rayon, qui coupe les perpendiculaires (1) et (2).
4. Tracez la parallèle reliant les points d’intersection C et D.

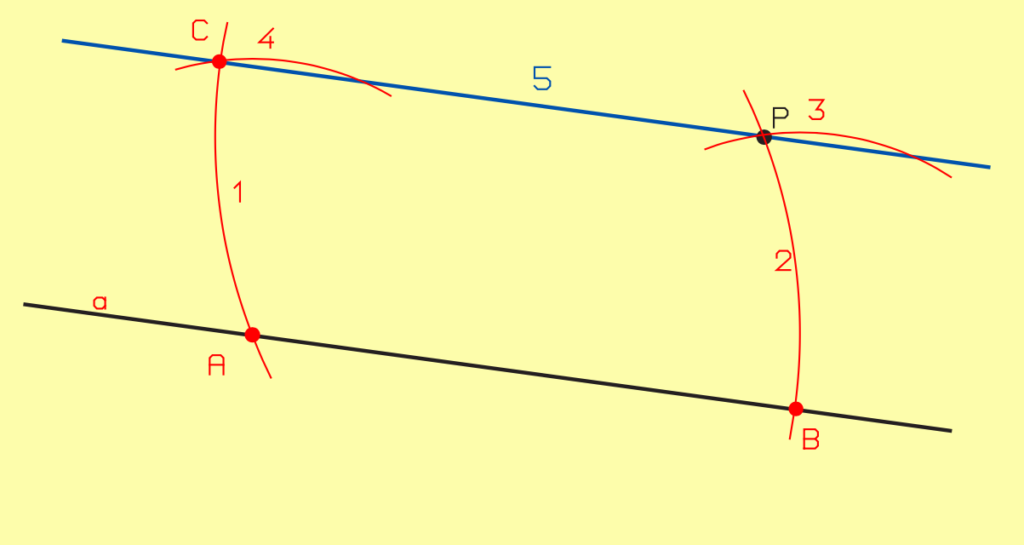
II.2.2.2. Parallèle passant par un point donné P

1. À partir du point P, tracez l’arc (1), de rayon quelconque, coupant la droite a.
2. À partir du point A obtenu, tracez l’arc (2), de même rayon, passant par P et coupant la ligne a.
3. En prenant la distance B-P comme rayon, tracez l’arc (3) depuis B.
4. Tracez l’arc (4), de rayon identique, depuis A.
5. Tracez la parallèle (5) à la droite a, en reliant P et le point d’intersection C.

II.2.3. DIVISIONS

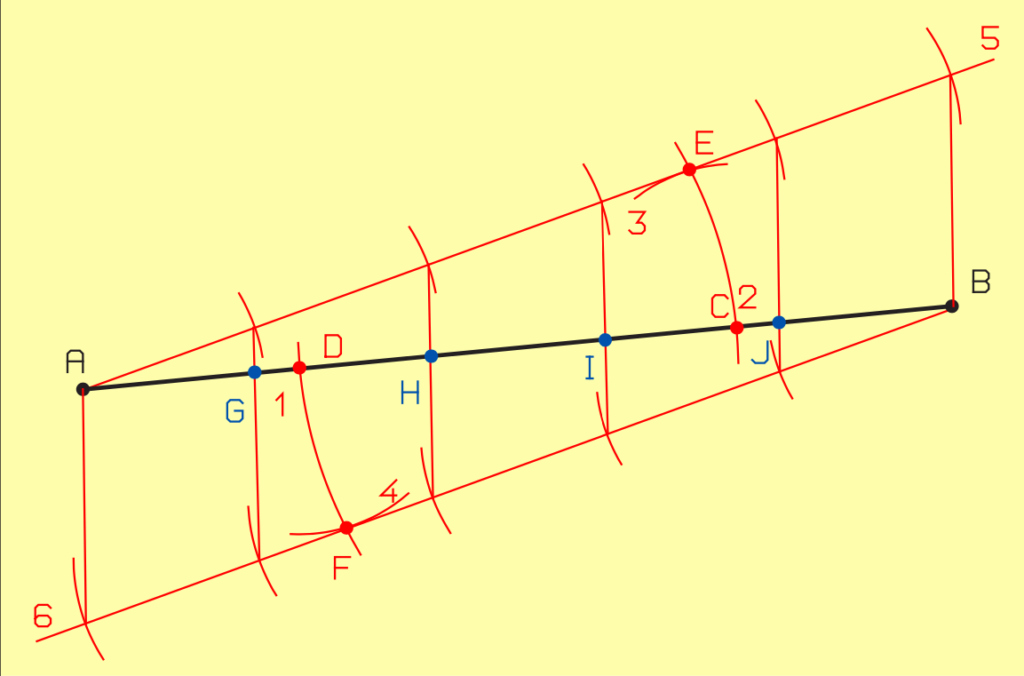
II.2.3.1. Diviser un segment de droite [AB] en n parties égales (p.ex. 5), méthode 1

1. Tracez l’arc 1, de rayon quelconque, à partir d’un point quelconque C.
2. Tracez l’arc 2, de rayon identique, à partir du point D.
3. À partir de C, tracez l’arc 3, de rayon quelconque.
4. À partir de D, tracez l’arc 4, de rayon identique.
5. Reliez A au point d’intersection E, à l’aide d’une ligne auxiliaire.
6. Reliez B au point d’intersection F, à l’aide d’une ligne auxiliaire.
7. À l’aide d’un rayon quelconque, reportez 5 segments égaux sur la ligne auxiliaire 5.
8. En conservant le même rayon, répétez l’opération sur la ligne auxiliaire 6.
9. Tracez les droites auxiliaires A – 1 6 , 7 – 1 5 , 8 – 1 4 , 9 – 1 3 , 1 0 – 1 2 , 11 – B .
10. Les points d’intersection G, H, I et J partagent le segment de droite AB en 5 parties égales.

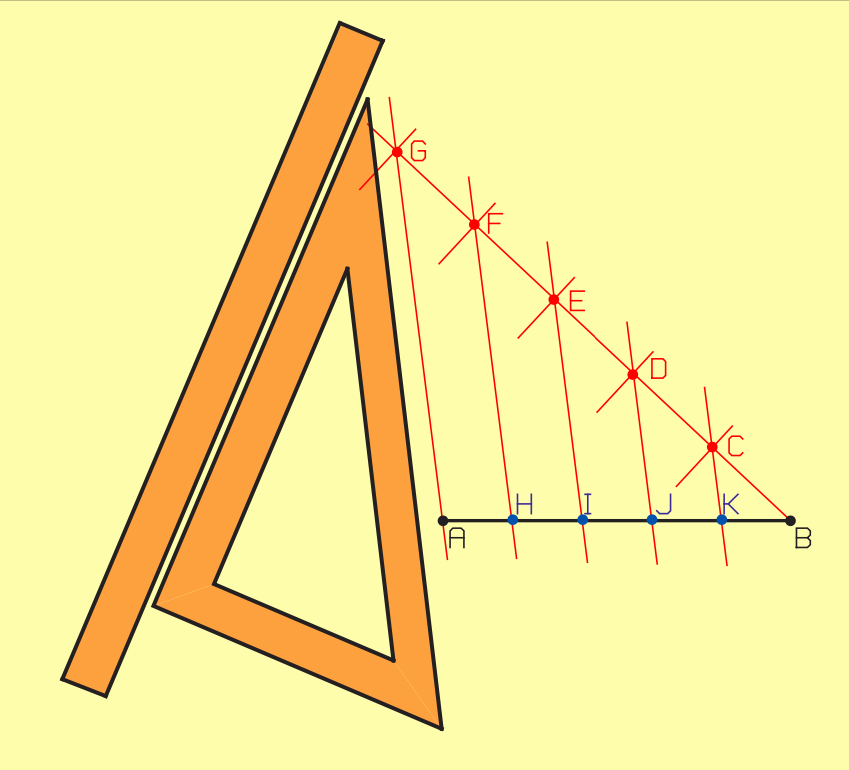
II.2.3.2. Diviser un segment de droite [AB] en n parties égales (p.ex. 5), méthode 2

1. Tracez une ligne quelconque à partir du point B et reportez-y une longueur facile à diviser (p.ex. 5 x 5 cm). On obtient ainsi les segments de droite BC, CD, DE, EF et FG.
2. Reliez G à A.
3. À l’aide d’une équerre et d’une latte, tracez un ensemble de parallèles à AG, passant respectivement par les points F, E, D et C.
4. Les points d’intersection avec AN (H, I, J et K) divisent le segment de droite AB en 5 parties égales.

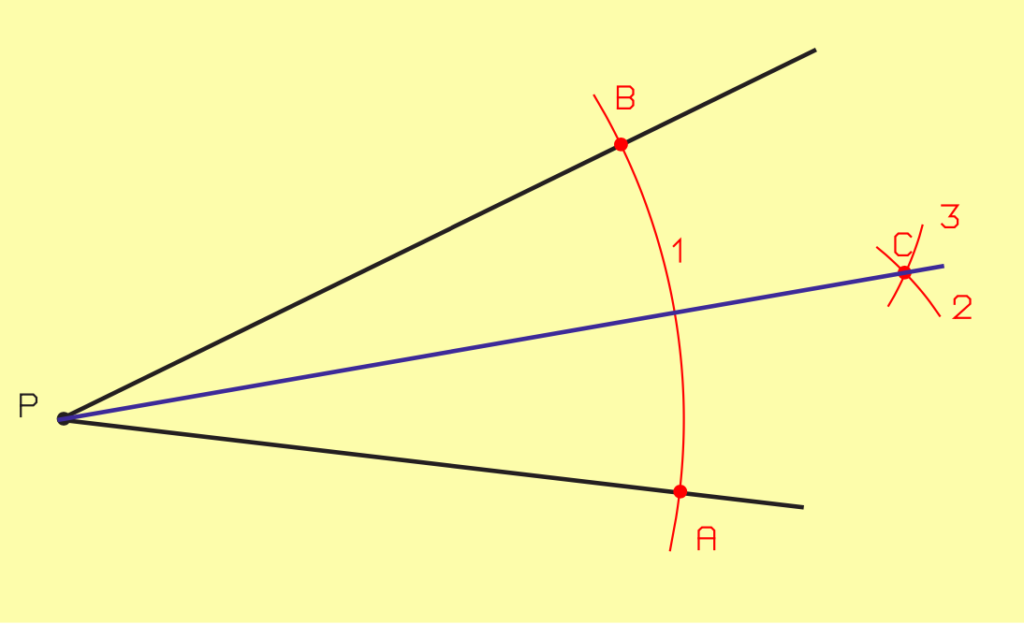
II.2.3.3. Division des angles

1. À partir du sommet P, tracez l’arc 1 de rayon quelconque.
2. Tracez l’arc 2, de rayon quelconque, à partir du point d’intersection A.
3. Tracez l’arc 3, de rayon identique, à partir du point d’intersection B.
4. Tracez la bissectrice reliant P au point d’intersection C.

II.2.4. TANGENTES ET POLYGONES RÉGULIERS

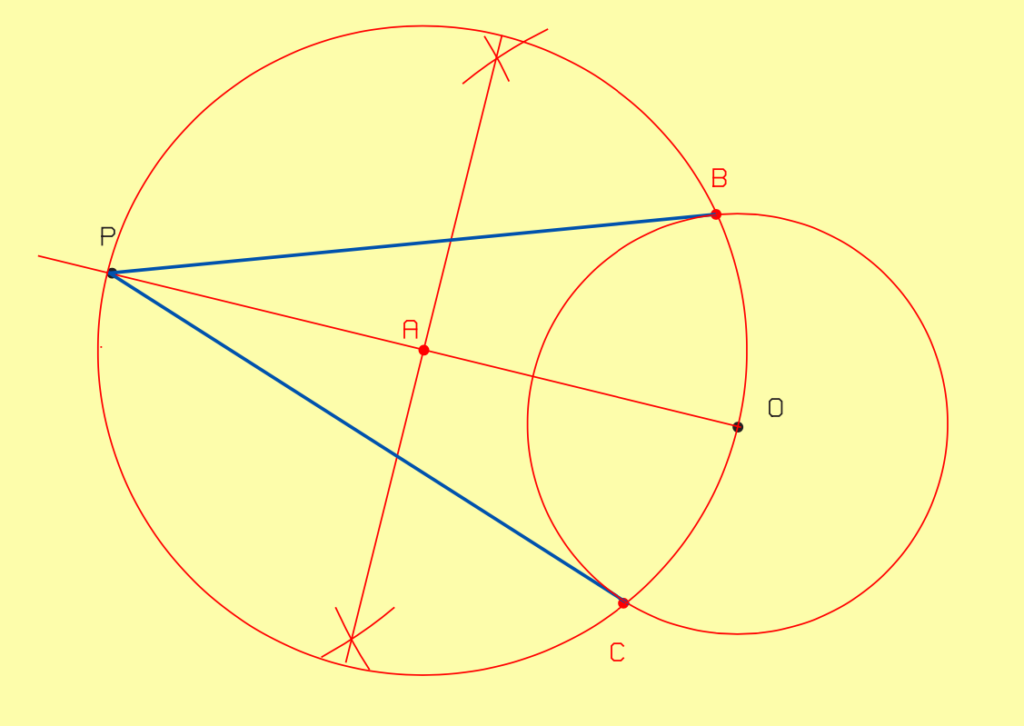
II.2.4.1. Tangente à un cercle à partir d’un point P

1. Reliez le point P au centre O.
2. Tracez la médiatrice du segment [OP].
3. Tracez un cercle ayant comme centre le point d’intersection A et comme rayon AO.
4. Les points B et C constituent les intersections des deux cercles.
5. Tracez les tangentes PB et PC.

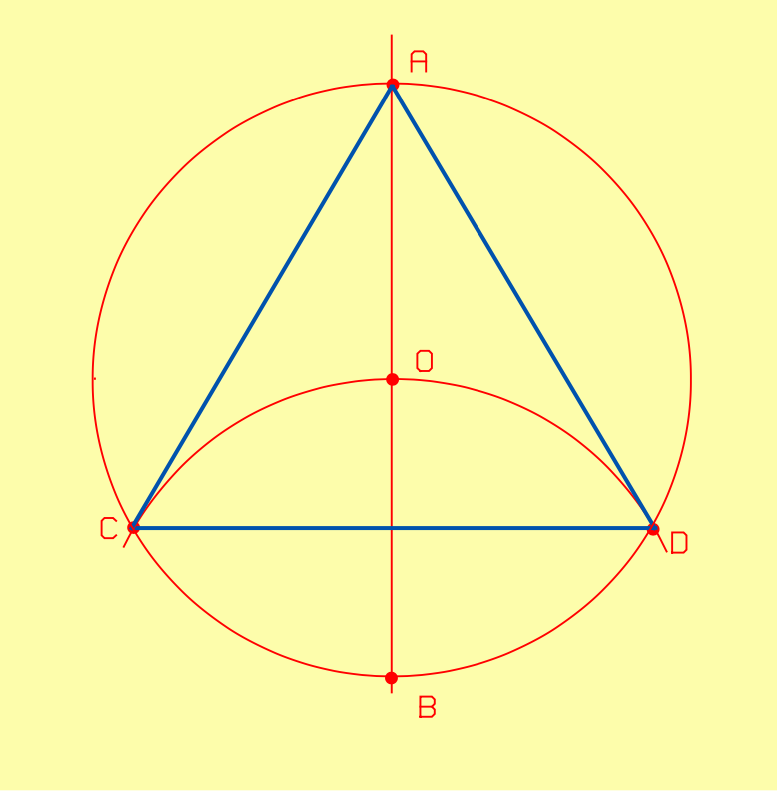
II.2.4.2. Triangle régulier inscrit dans un cercle

1. Tracez la droite AB passant par le centre O du cercle donné.
2. À partir de B, tracez un arc de rayon égal à celui du cercle.
3. Cet arc coupe le cercle en C et D.
4. Tracez le triangle A – C – D.

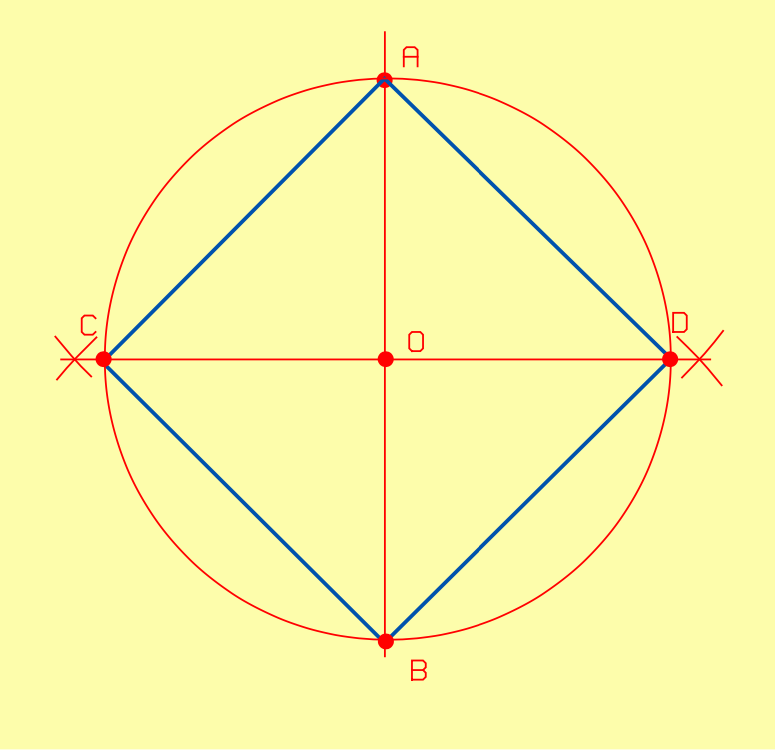
II.2.4.3. Quadrangle régulier inscrit dans un cercle

1. Tracez la droite AB passant par le centre O du cercle donné.
2. Tracez la médiatrice CD à la droite AB au point O.
3. Tracez le carré A – B – C – D.

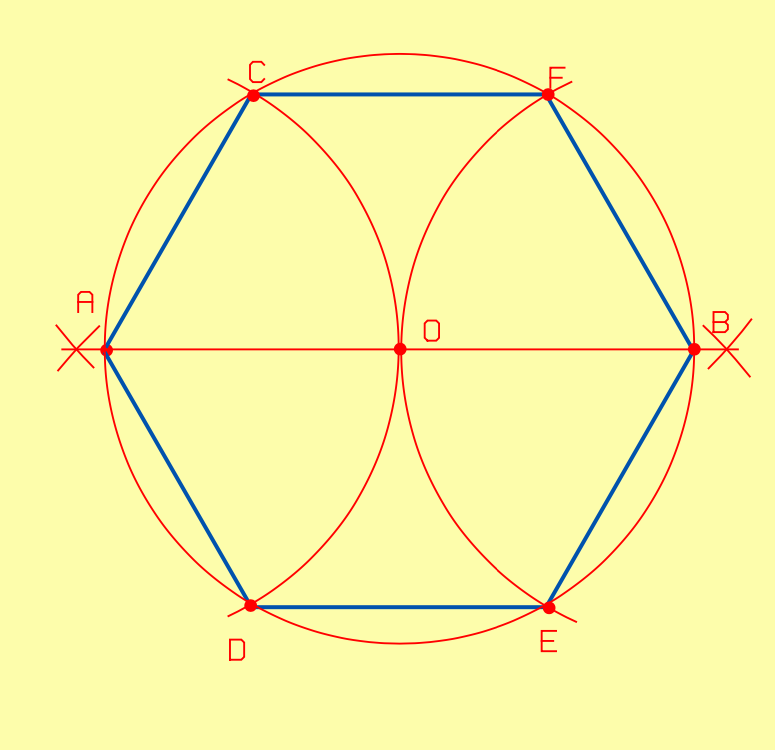
II.2.4.4. Hexagone régulier inscrit dans un cercle

1. Tracez la droite AB passant par le centre O du cercle donné.
2. À partir du point A, tracez un arc dont le rayon est égal à celui du cercle.
3. Cet arc coupe le cercle aux points C et D.
4. À partir du point B, tracez un arc dont le rayon est égal à celui du cercle.
5. Cet arc coupe le cercle aux points E et F.
6. Tracez l’hexagone A – C – F – B – E – C.

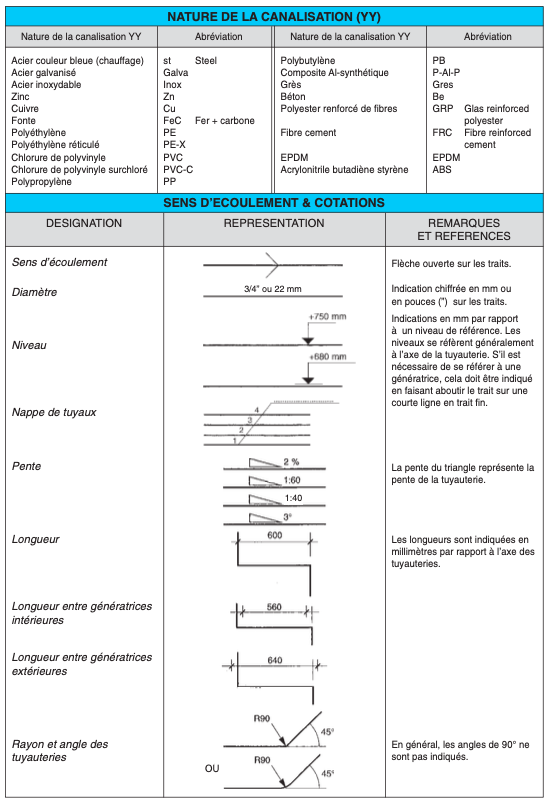
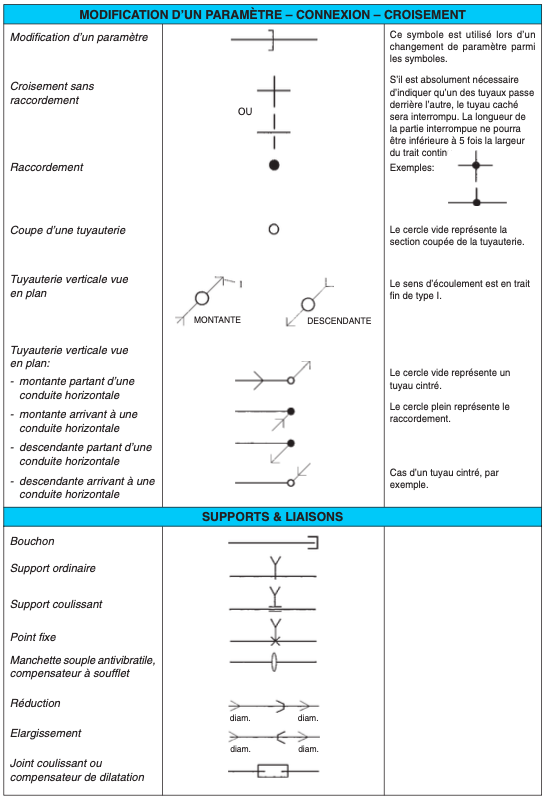
II.3. REPRÉSENTATION DES SYMBOLES SANITAIRES (*)

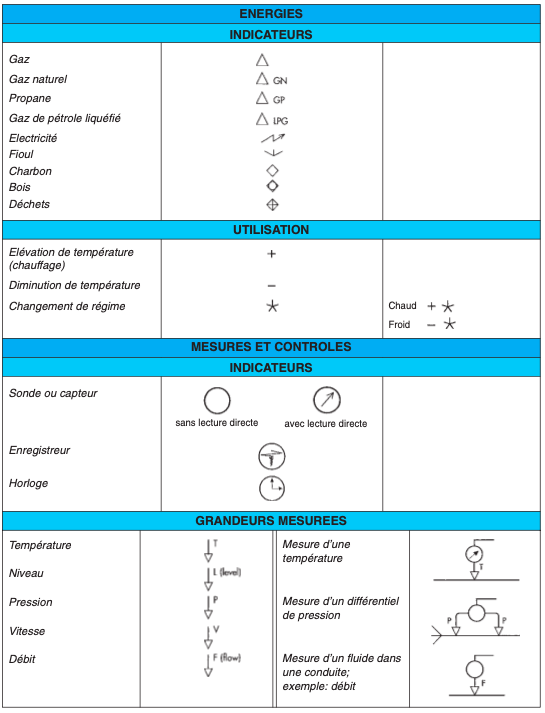
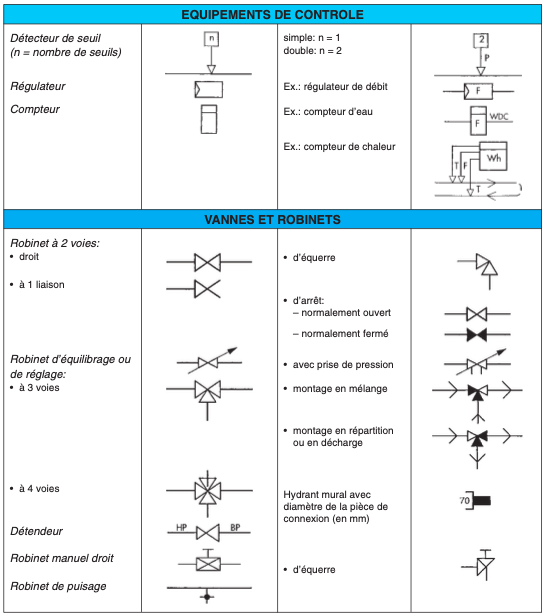
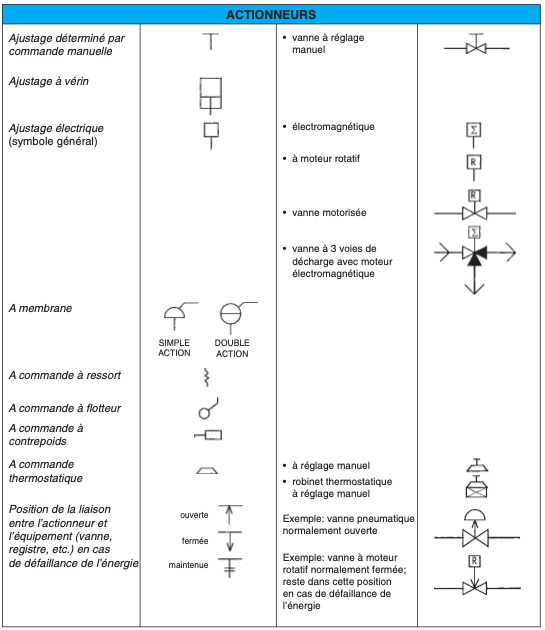
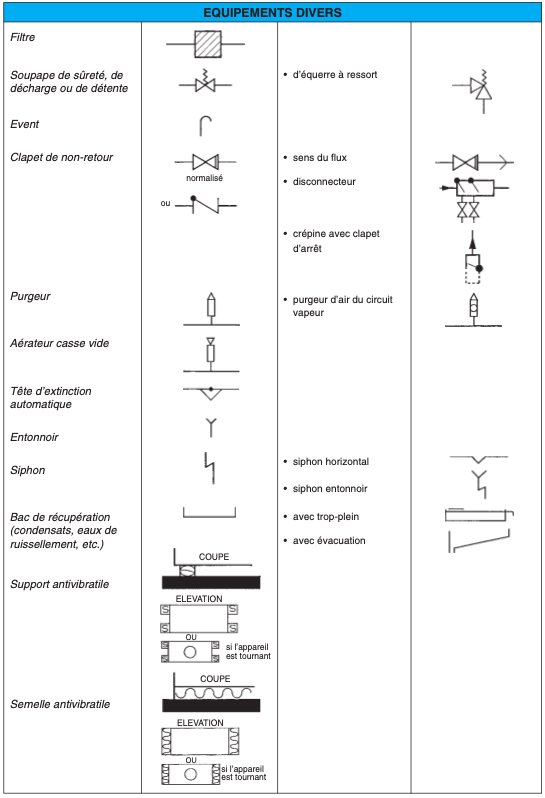
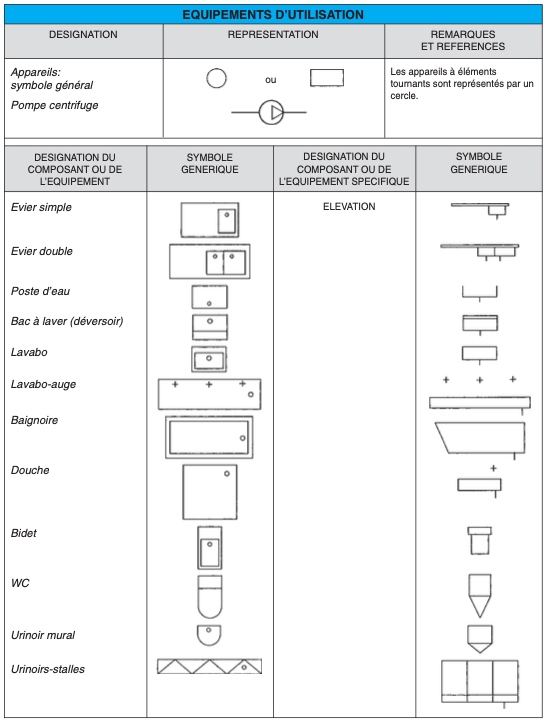
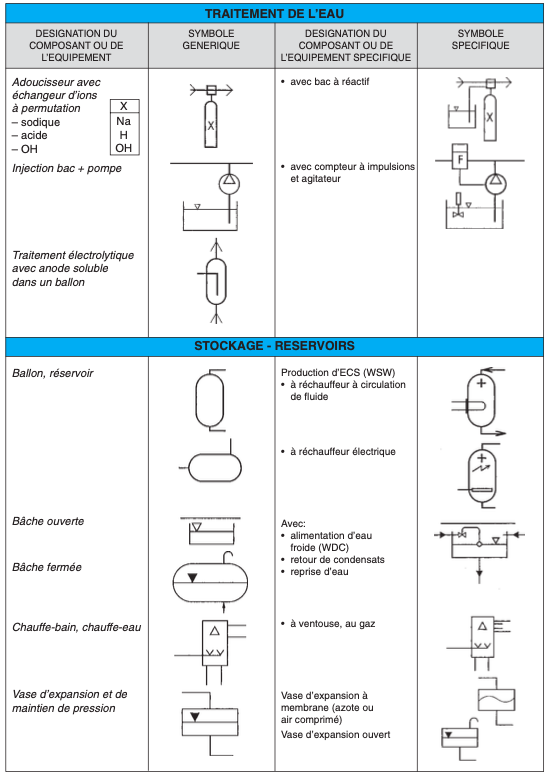
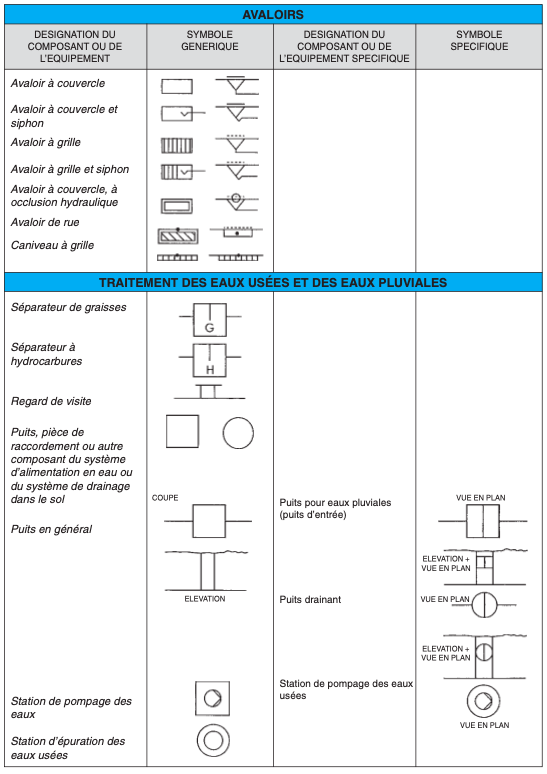
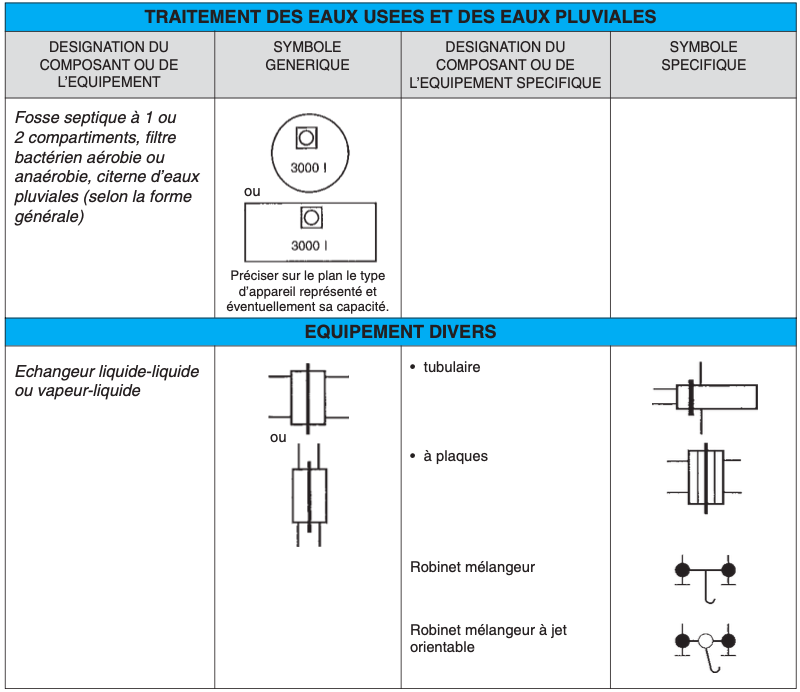
II.4. LECTURE DE PLANS (plans en annexe)

Deux plans de construction sont annexés au “Module II – DESSIN: LECTURE DE PLANS”.

Les quelques questions ci-dessous devraient inciter à apprendre à lire ces plans.

• Quelle méthode de projection a-t-on utilisé pour le dessin des vues?
• S’agit-il d’une maison de rangée ou d’une construction isolée?
• Est-ce visible sur les murs extérieurs?
• Quelle est la différence entre un mur de cloison et la façade avant?
• Quel est le nombre d’étages habitables de ce bâtiment?
• Dispose-t-il d’un vide sanitaire? Sur quelle partie du plan fi gure-t-il?
• Une citerne d’eau de pluie est-elle prévue?
• Combien de fenêtres de toiture sont-elles prévues?
• Y a-t-il une coupole dans la cuisine? Quel diamètre a-t-elle et sur quelle partie du plan fi gure-t-elle?
• Combien y a-t-il de W.C. dans ce logement?
• Combien de portes intérieures faut-il commander? Quelles sont leurs dimensions?
• À quelle heure environ le premier rayon de soleil pénètrera-t-il par la fenêtre de la cuisine?
• Calculez la surface et le volume de la salle de bains.
• Les conduites sanitaires ne sont généralement pas dessinées dans le cas de petites constructions, telles que celle-ci. On laisse habituellement ce soin au savoir-faire de l’installateur. Prenez une copie des coupes concernées et essayez de dessiner les amenées d’eau chaude et froide.

N’oubliez pas les gaines techniques qui peuvent être utilisées.

Nous supposons que l’eau chaude est préparée dans la chaufferie. Est-il raisonnable d’alimenter la cuisine à l’aide de cette eau chaude? Y a-t-il d’autres possibilités? Pourquoi faut-il faire un choix à ce stade?

Établissez enfi n un métré quantitatif.

Concevez éventuellement une autre salle de bains.

Les dessins isométriques des évacuations de cette maison sont représentés ci-après. Si la lecture du chapitre suivant est nécessaire à la bonne compréhension de ce plan, la façon dont les évacuations doivent être réalisées s’y voit assez clairement sans cette théorie.

II.5. DESSIN ISOMETRIQUE

II.5.1. CONVENTIONS

Dessins de tuyauteries selon la «MÉTHODE DE PROJECTION ISOMÉTRIQUE»

BUT:

• Obtenir une représentation du dessin d’installation sur laquelle figurent clairement la forme et les dimensions, sans qu’il soit nécessaire de réa- liser plusieurs vues.

Avantage:

• Le travail de dessin est réduit.
• On visualise très rapidement à quoi ressemblera l’installation. Le plan est plus aisé à lire si l’on sépare le dessin de l’installation en dessins spécifiques de chaque partie de l’installation telles que le gaz, l’eau chaude et froide, les égouts et l’évacuation de l’eau de pluie.

Principe:

• Trois plans sont représentés sur une feuille de papier plane.
• On dessine selon trois directions principales.
• Les trois directions forment entre elles des angles égaux (iso = égal).
• On utilise du papier isométrique pré-imprimé

II.6. CROQUIS

• L’établissement de croquis est l’un des aspects les plus importants du dessin technique. Un croquis donne souvent de meilleurs résultats qu’une longue explication orale ou écrite.
• Les croquis sont dessinés à main levée, à l’aide d’un crayon à mine n° 2 ou plus tendre.
• Un croquis permet de représenter rapidement un dessin ou un détail.
• Il donne une première impression de l’ouvrage que l’on veut dessiner en détails.
• Un croquis tridimensionnel donne une représentation dans l’espace du travail à réaliser.
• Un croquis permet souvent de déceler une partie des problèmes et de modifier l’idée de départ. De cette façon, ces modifications ne devront plus être apportées ultérieurement au stade du dessin.
• A l’aide des différents croquis, on réalise le dessin technique.

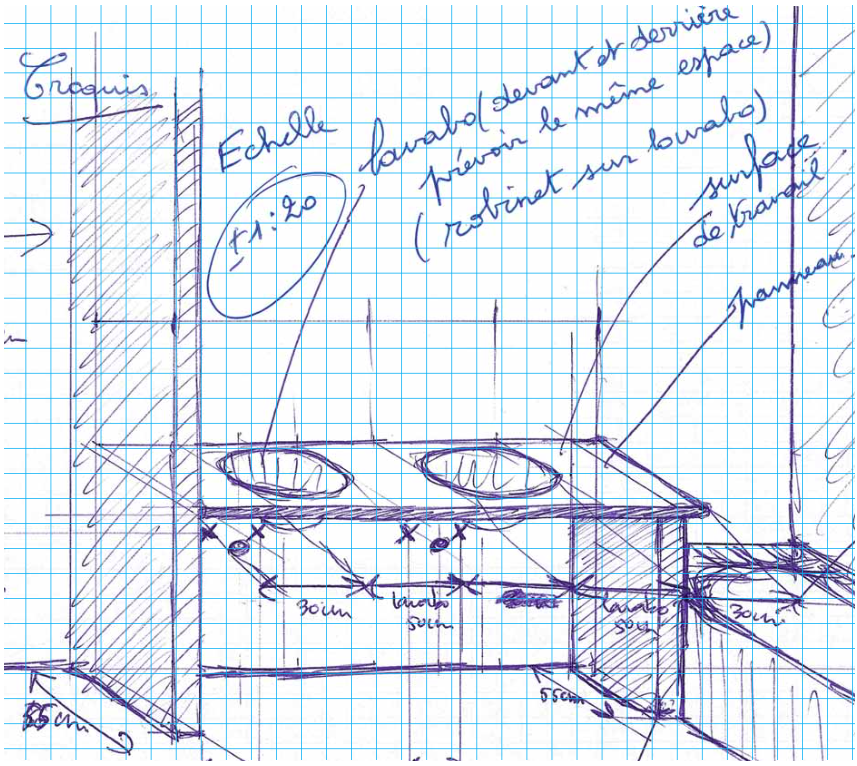
Ce croquis, à première vue simple, doit répondre à quelques règles de base, de telle façon que la personne qui aura la charge de le réaliser ne puisse pas commettre d’erreur.

L’échelle du plan de projection est de 1:20, le troisième axe de coordonnées est dessiné selon un angle de 45°.
Les lignes de projection obliques sont réduites aux 2/3 (parfois à 1/2, car cette méthode est plus rapide), de façon à conférer un aspect plus naturel à la perspective.

De cette manière, avec un peu d’entraînement, on réalise rapidement des croquis qui ont le mérite d’être très clairs.

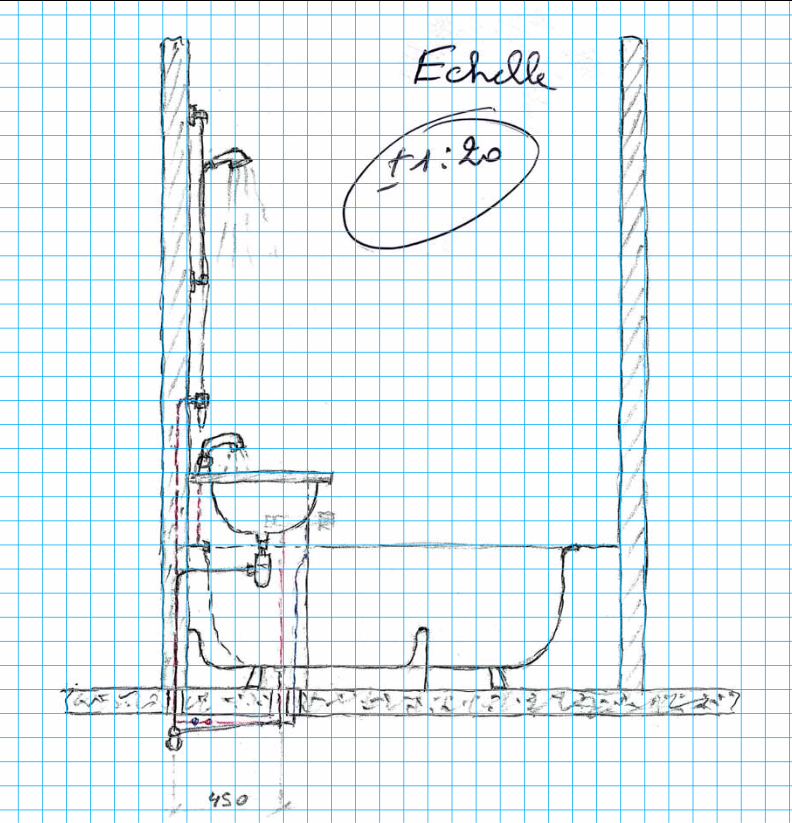
Il est évidemment possible d’étoffer davantage le croquis et de lui ajouter plus de détails.
Tout dépend de la personne qui devra exécuter le travail et du message à lui faire passer.
Il est cependant clair que plus le schéma sera précis, plus faible sera le risque d’erreur lors de l’exécution.

Quelques exemples

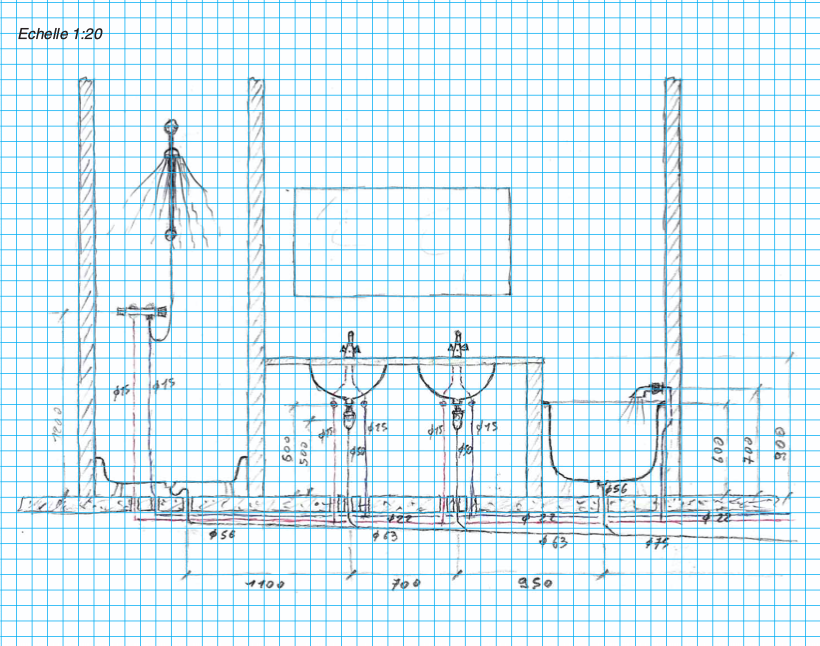
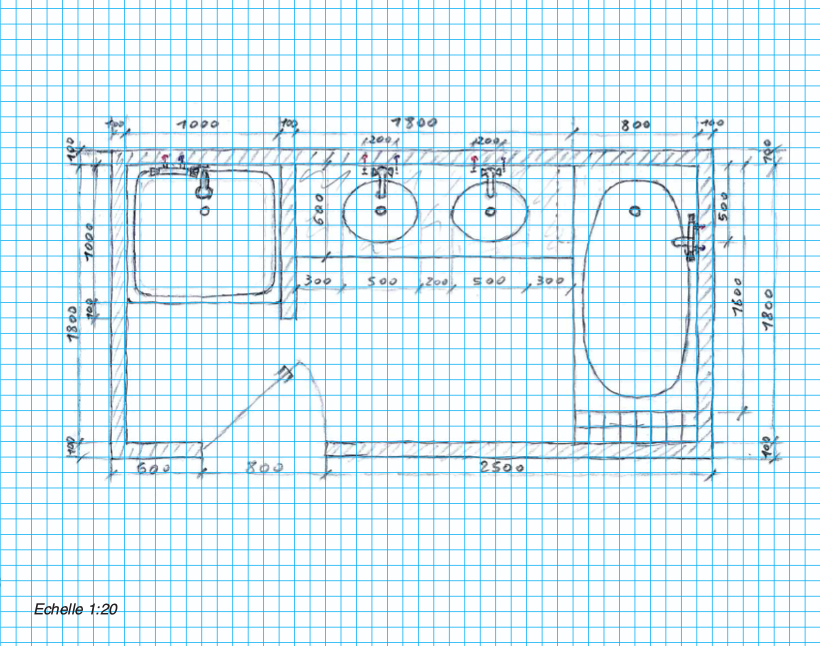
II.7. DESSIN FONCTIONNEL SUR ORDINATEUR

II.7.1. DU DESSIN A LA SIGNIFICATION

II.7.1.1. Historique

Un peu d’histoire

Afin de comprendre comment se sont développés les systèmes de CAD (Computer Aided Design – en français, on dit aussi DAO, Dessin Assisté par Ordinateur), il est bon de se pencher sur l’histoire de l’utilisation du dessin.

En fait, nous pourrions commencer comme dans un conte: “Il était une fois un homme qui avait une idée et qui voulait la réaliser”.

Et c’est ce qu’il fit.

Au temps où la technique était simple, il était encore relativement aisé de réaliser ses idées par soi-même. Les avancées techniques, comme les inventions, ont ainsi souvent été matérialisées personnellement par leurs concepteurs. Les dessins de cette époque n’étaient souvent que de simples aide-mémoire à l’usage du concepteur/exécutant.

Il suffisait que le concepteur puisse comprendre son propre dessin et il n’était pas nécessaire que les autres le comprennent.

Le dessin a également permis de représenter clairement des idées qui, à l’époque, ne pouvaient pas encore être mises en œuvre, tel l’hélicoptère de Léonard de Vinci.

II.7.1.2. Dissociation concepteur-exécutant

Plus les projets ont pris de l’envergure, plus les concepteurs ont éprouvé des difficultés à réaliser seuls leur projet.

Cette évidence est vite apparue dans le secteur de la construction. Une seule personne suffisait pour monter une hutte, mais par pour construire une cathédrale par exemple. Il a fallu partager son idée avec d’autres afin que ceux-ci puissent contribuer à sa réalisation.

Au départ, les instructions passaient oralement. L’architecte était présent sur le chantier et donnait ses ordres aux corps de métier chargés d’exécuter les travaux.

Cette façon de travailler est possible pour autant qu’il y ait une communication directe entre le concepteur et l’exécutant et qu’il s’agisse d’instructions relativement simples.

II.7.1.3. Le dessin en tant que document

La complication croissante des techniques de construction a modifié cette situation.

Il a donc fallu consigner les instructions (le projet) sur papier, d’une façon telle que des tiers puissent les comprendre. Cette nécessité se faisait surtout sentir quand le concepteur n’était pas disponible pour répondre aux demandes de renseignements.

Le dessin technique était une réponse à ce besoin.

La situation s’est encore compliquée quand le concepteur a commencé à faire exécuter son projet par d’autres – souvent à la demande du maître de l’ouvrage – au lieu de le réaliser lui-même.
Les différentes parties impliquées dans un projet se sont vues forcées de conclure des accords mutuels. C’était un document dans lequel étaient stipulés les matériaux à utiliser, mais aussi à quel prix devait être réalisé le projet.

Ces documents ont acquis le statut de contrat, de convention.

Le dessin a commencé à faire partie des pièces contractuelles et est parfois même devenu la pièce la plus importante du contrat.

Étant donné les possibilités techniques de l’époque, le dessin consistait en une série de lignes et de textes tracés à la main sur une feuille de papier, de la même façon qu’un document textuel consistait en un texte manuscrit sur une même feuille de papier.

II.7.1.4. Conventions uniformes

Pas de communication sans conventions

Il est apparu assez rapidement que les dessins n’apportaient pas tous les éclaircissements requis. Ce qui était consigné sur papier par le concepteur (le dessinateur) n’était pas toujours bien compris par la personne chargée de réaliser le projet.
Comme, à l’époque, le dessin faisait partie du contrat, ceci occasionnait des problèmes. Cette situation n’a rien de révolu: à l’heure actuelle, elle génère encore toujours son lot d’ennuis.
Pour qu’un dessin serve le but dans lequel il est réalisé, il doit être clair et univoque.
Univoque signifie que le dessin n’accepte qu’une seule interprétation.
Il existe une ambiguïté quand il est possible de réaliser deux choses différentes sur base du même dessin et que ces deux interprétations correspondent bien au plan.
Ce besoin d’univocité a conduit à la nécessité d’établir des conventions. Qu’il s’agisse d’un mur, d’une porte ou d’une vanne, il faut que les lignes représentées sur le plan soient perçues en tant que mur, porte ou vanne par la personne qui réalise le travail.
C’est pourquoi il a été convenu qu’un mur était représenté sur un plan par son périmètre, complété par des hachures, déterminant le matériau dans lequel est construit ce mur.

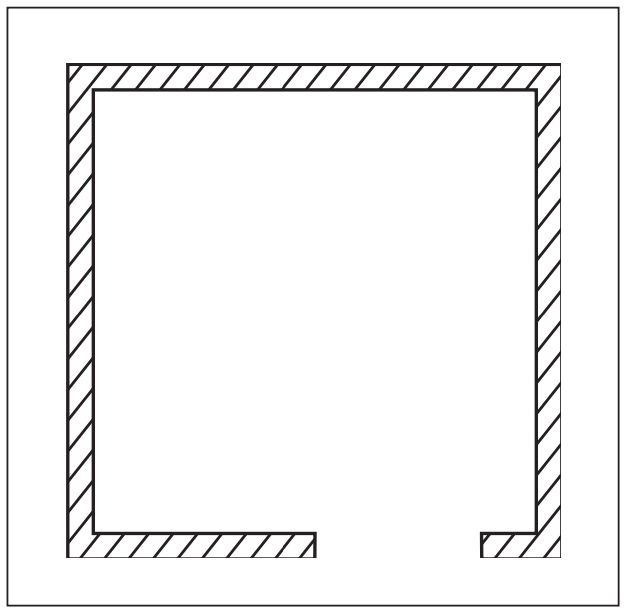
Pour une porte, la convention est à peu près la même, à cette différence près que l’on ajoute un quart de cercle, indiquant si le battant s’ouvre à gauche ou à droite. Si le reste des traits représente une image réduite de la réalité, le quart de cercle est purement symbolique. Si vous visitez un chantier, vous ne verrez pas ce quart de cercle marqué au sol. On a décidé d’indiquer le sens de rotation à l’aide d’un symbole.

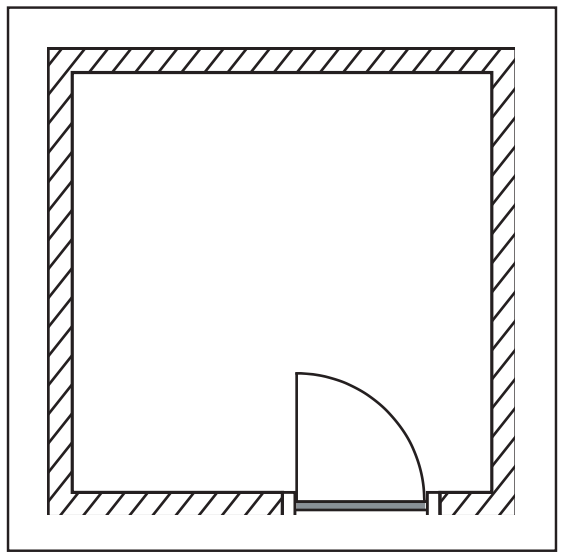
On aurait pu également convenir que la porte devait toujours être représentée ouverte, auquel cas le quart de cercle n’aurait pas eu de raison d’être. On a cependant évité cette convention, qui n’aurait pas favorisé la clarté du plan.

Un symbole est donc une représentation simplifiée et univoque d’une certaine réalité. Pour simplifier, on utilise un symbole pour représenter quelque chose qui, autrement, serait soit trop compliqué ou peu clair.

Ce point est encore plus évident dans le cas de la vanne.

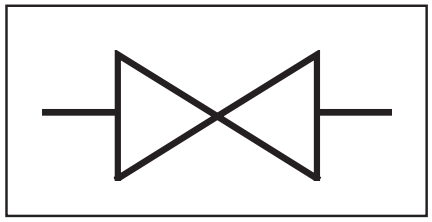
On utilise un symbole relativement simple pour représenter une vanne dans les dessins schématiques. On aurait évidemment pu représenter une vanne réelle, mais le dessin aurait pris beaucoup plus de temps, sans pour autant gagner en lisibilité.
C’est encore plus évident quand on sait qu’il existe de nombreux types de vannes. Il n’est même pas garanti que l’on puisse déterminer le type de vanne exact à partir de son dessin complet, mais quelques lignes supplémentaires adjointes au symbole suffisent pour lever toute ambiguïté.
Si une personne non au courant des conventions peut encore reconnaître une porte indiquée sur un plan parce que sa représentation ressemble à une porte, ce n’est certainement plus le cas avec une vanne.

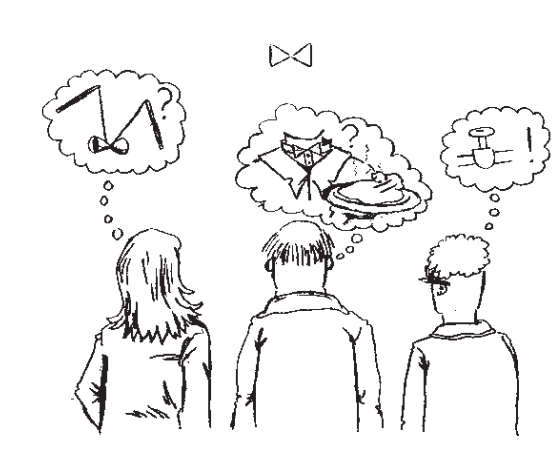
Un enfant des années ’30 du siècle passé aurait pensé qu’il s’agissait d’un diabolo (un jouet), quelqu’un d’autre y aurait vu un nœud papillon et un habitant de Papouasie Nouvelle-Guinée n’y aurait rien vu du tout. Il est important de se rendre compte qu’un symbole n’acquiert une signification que lorsque toutes les parties se sont mises d’accord à son sujet.

II.7.2. ÉVOLUTION

II.7.2.1. Du crayon électronique …

C’est à ce moment que l’ordinateur entre en scène. Il le fait aux environs de 1970 dans les universités et les centres de recherche, et dans les années ’80, dans la vie de tous les jours.
Très vite, l’ordinateur sera utilisé pour le traitement de textes, en remplacement de la machine à écrire. Par rapport à la machine à écrire, l’ordinateur présente l’avantage de faciliter les corrections et permet la conservation des documents. D’autres fonctions, comme la pagination et la table des matières automatique ou le correcteur orthographique viendront plus tard encore augmenter ses capacités. À l’époque, la réalisation de dessins techniques par ordinateur a suivi le même cheminement.

Les programmes CAD (computer aided design, en français CAO: conception assistée par ordinateur) apparaissent sur le marché, mais ils ne sont, en fait, que des programmes de traitement de textes appliqués à des lignes, un simple crayon électronique. Le D signifie plus Drafting (dessin) que Design (conception). Même si ces programmes possédaient déjà des fonctionnalités plus étendues à l’époque, celles-ci sont peu utilisées dans la pratique de tous les jours. Devant son écran, le dessinateur travaille en réalité de la même façon que son collègue à sa table à dessin. Il trace des lignes, des cercles et des textes. Les atouts de l’ordinateur sont similaires à ceux du traitement de texte: corrections aisées et sauvegarde des plans.
Les fonctions copier, déplacer et modifier présentaient de grandes similitudes avec les actions correspondantes en traitement de texte. Les fonctions de visualisation, telles que le grossissement, la réduction ou le déplacement ne sont pas foncièrement différentes de celles prévues dans d’autres logiciels.

Dans les programmes de dessin, la pagination automatique, la table des matières automatique et le correcteur orthographique du traitement de textes sont remplacés par les hachures, les textes et les lignes de cotes automatiques. Tout ceci facilite la vie du dessinateur. Tant et si bien qu’en l’espace de 20 ans (de 1980 à 2000) le dessin assisté par ordinateur se substitue quasiment à la méthode de dessin classique à la table à dessin.

Cependant, et malgré ces changements énormes, le processus du dessin n’a pas été fondamentalement modifié. Le dessin présente le même aspect qu’auparavant et se base sur les mêmes conventions. Plus important encore: le dessin n’a de signification que pour ceux qui en connaissent

les conventions. Notons encore que l’ordinateur n’est pas une personne et n’est donc pas à même de comprendre ces conventions. Pour un ordinateur, il n’existe que des lignes, des arcs de cercle, des textes et des dimensions. Mais pas de portes, de murs ou de vannes.

II.7.2.2. … via les icônes …

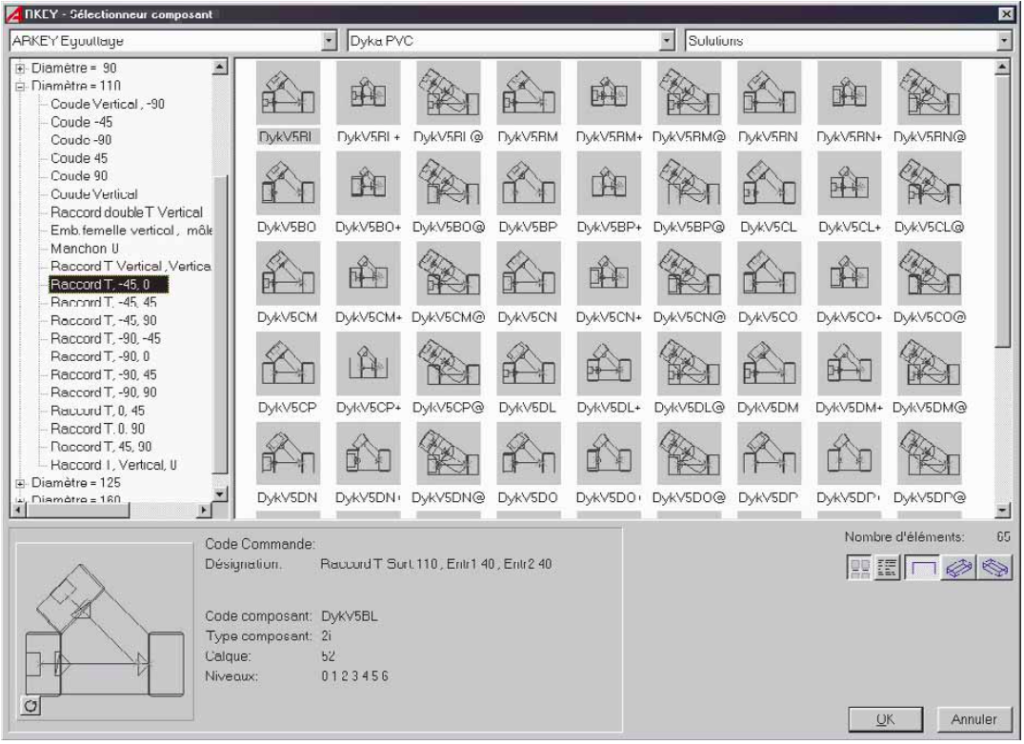
Un élément important de la percée des logiciels de dessin par ordinateur tient aux bibliothèques de composants et de symboles.
Il s’agit de collections de dessins préétablis relatifs à toutes sortes d’éléments de construction ou d’installations techniques.
Grâce à l’apparition de ces bibliothèques sur le marché, le dessinateur ne doit plus dessiner lui-même ses portes ou ses vannes. Il lui suffit de les extraire de la bibliothèque et de simplement les placer dans son dessin. Une telle bibliothèque constitue, en fait, une énorme boîte à icônes comprenant des centaines, voire des milliers d’icônes. Ces icônes sont pareilles aux dessins et symboles dessinés manuellement et répondent aux mêmes conventions de dessin.
L’utilisation de l’ordinateur semble donc procurer une certaine amélioration, mais il s’agit plus d’une apparence que d’une réalité.
Même si la vanne n’est plus actuellement représentée par quatre lignes indépendantes, mais bien par des lignes associées au sein d’un symbole, le niveau d’intelligence de l’ordinateur n’a pas réellement augmenté. S’il ne voit plus des lignes, mais bien un symbole, pour lui, ce n’est cependant rien d’autre qu’une icône répondant à un certain nom.

Beaucoup de systèmes de dessin peuvent compter les icônes et permettent donc de cette façon d’établir le métré quantitatif, sous la forme d’un relevé sur lequel il apparaît que 3 pompes et 7 vannes figurent sur un plan donné.
Ce relevé sera peut-être utile à un être humain, mais pour l’ordinateur, il ne s’agit que d’un décompte des icônes utilisées.
Un simple exemple nous permettra de mettre en lumière les problèmes qui peuvent surgir. Si, par malheur, le dessinateur a placé deux symboles exactement l’un sur l’autre, il ne le verra pas, mais la liste comprendra un symbole de trop par rapport au nombre de symboles visibles.
Le décompte effectué sur l’écran ou sur papier sera exact, le décompte réalisé par l’ordinateur sera correct pour l’ordinateur mais pas pour l’être humain. C’est pour cette raison que le relevé n’est pas fiable et que, la plupart du temps, il est inutilisable.

II.7.2.3. … et les applications…

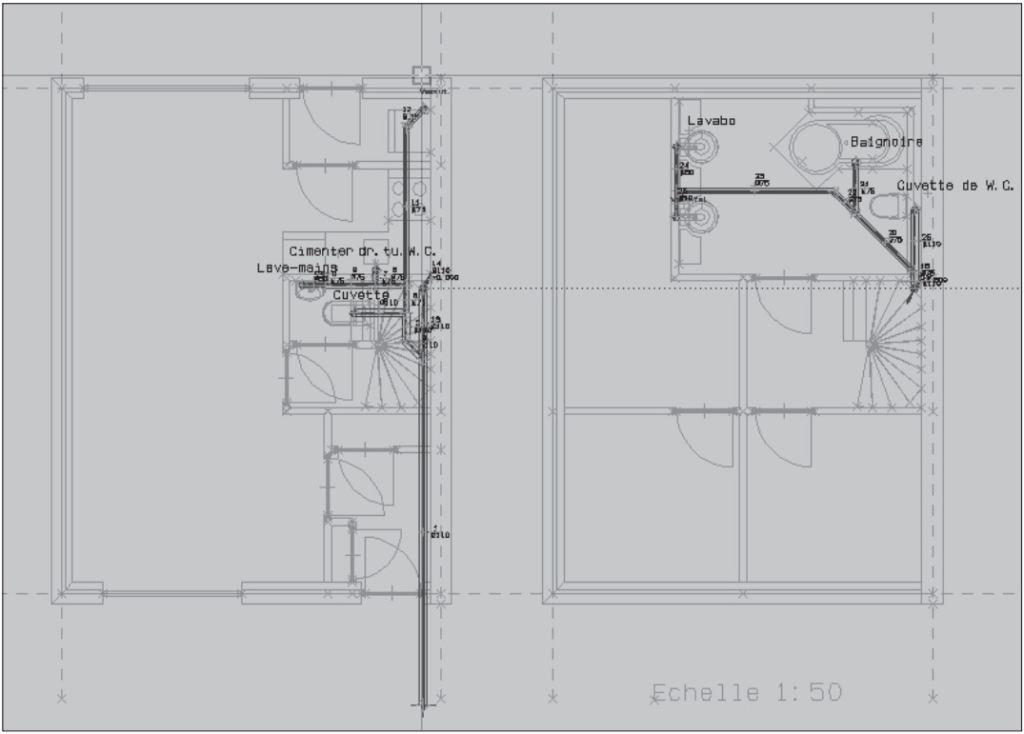
Afin de résoudre ce genre de problèmes et de conférer une certaine signification aux éléments dessinés, on a développé ce que l’on appelle des applications.
Une application est un ensemble cohérent de fonctions et de bibliothèques qui rendent un logiciel de dessin généraliste mieux apte à la réalisation d’un type de dessin particulier.
Une application pourrait, par exemple, comporter une fonction permettant de détecter les symboles placés en double (voir plus haut) et d’en supprimer les exemplaires superflus.
De cette façon, le relevé des pièces pourrait être utilisable.
Une application pourrait également permettre d’étendre les possibilités du logiciel de dessin à un endroit donné, ou, au besoin, de les restreindre.

Un certain nombre de logiciels de dessin (p.ex. ceux qui ne sont pas spécifiquement prévus pour la construction) ne présentent pas la possibilité de mémoriser le symbole d’un mur dans leur bibliothèque et de disposer ensuite ce symbole de toutes sortes de manières (p.ex. en angle ou en arc).
Et ne parlons même pas de la possibilité de créer une baie dans le mur afin d’y placer une porte ou une fenêtre.« 

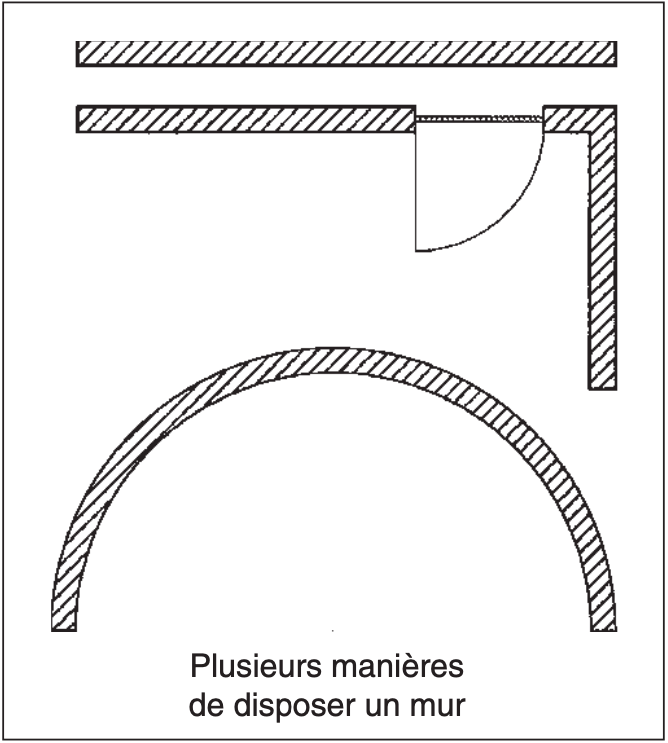
Une fonctionnalité peut enfin être intégrée dans une application afin de satisfaire les demandes d’une profession particulière. Il peut parfois être nécessaire de limiter les fonctionnalités standard du logiciel afin de ne pas autoriser des représentations que ce dernier peut réaliser, mais qui, en réalité, sont impossibles.

Nous prendrons comme exemple la possibilité de redimensionner les symboles, c’est-à-dire d’en agrandir ou d’en réduire la représentation. Supposons que nous ne disposions que du symbole représentant une baignoire de 80 x 160 cm.

Mais le dessinateur a besoin d’une baignoire de 90 x 180 cm, donc un peu plus grande. Pas de problème, il prend le symbole de 80 x 160 cm et l’étire jusqu’à 90 x 180 cm. Sur le dessin apparaît bien une baignoire de 90 x 180 cm, mais le relevé spécifie une baignoire de 80 x 160 cm et est donc faux.

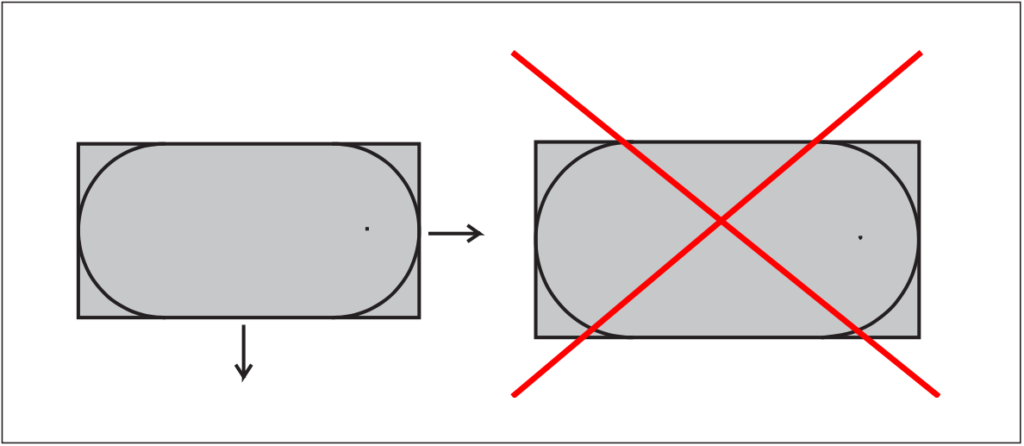
Une application peut intégrer une fonctionnalité permettant de détecter une baignoire étirée et d’enjoindre au dessinateur de choisir une autre baignoire (dont les dimensions font réellement 90 x 180 cm).

Il est évident que les vrais problèmes commencent quand, sur la base du relevé, on a commandé une mauvaise baignoire et qu’elle est livrée. L’installateur devra être réellement costaud pour étirer une baignoire de 80 x 160 cm aux dimensions nécessaires de 90 x 180 cm.

Il est évident que l’apparition des applications a élevé le niveau de connaissance des logiciels de dessin. Cette meilleure connaissance se limite toutefois, le plus souvent, à ce qui est nécessaire pour supporter le processus de dessin.
D’un mur, on connaît uniquement les données nécessaires pour le dessiner, mais cela ne suffit pas. Les relations entre les différents éléments sont souvent ignorées.

Un inconvénient important réside également dans le fait que cette connaissance ne va pas plus loin que l’application concernée.

Les murs, les portes et les vannes d’une application ne sont, pour l’ordinateur, pas identiques aux murs, portes et vannes provenant d’une autre application, même si ces applications sont basées sur le même logiciel de dessin.
Ceci signifie également que les dessins réalisés à l’aide de l’application A peuvent bien être lus avec le logiciel sur lequel l’application A est basée, mais ne peuvent être modifiés en l’absence de cette application.

Du fait de cette limitation, les utilisateurs d’un même logiciel de dessin ne peuvent pas partager les informations générées s’ils n’utilisent pas la même application. Et, comme les applications se limitent souvent à un corps de métier spécifique, l’échange de ces informations supplémentaires entre différents corps de métier est en fait impossible.

II.7.2.4. … vers une nouvelle génération de systèmes CAD

Ce problème, et le souhait de lui apporter une solution, ont entraîné la nécessité de développer une nouvelle génération de systèmes CAD. Il s’agit, en fait, de systèmes où le D de CAD ne signifie plus Drafting (dessin) mais bien Design (projet), comme on le souhaitait au départ.
Ceci signifie que les systèmes CAD doivent évoluer en systèmes où la signification et les caractéristiques des éléments de bâtiments ou d’installations doivent être consignées.
On expliquera plus facilement ce que cela sous-entend à l’aide d’un exemple, pris ici dans le domaine de la technique d’installation sanitaire.
Supposons que nous devions concevoir le réseau interne de canalisations d’égout d’un immeuble.
Traditionnellement, le processus de conception aurait débuté par un plan sur lequel les appareils sanitaires auraient été dessinés.
Sur ce plan, le dessinateur reconnaît une baignoire, un W.C., un lavabo, etc.
En se basant sur son expérience professionnelle, il dessine les canalisations ainsi que les raccordements prévus à l’aide de lignes.
Il doit maintenant déterminer les diamètres des différents éléments de la tuyauterie. Ceci peut se faire sur la base de son expérience ou par un calcul.

Ce calcul peut s’effectuer manuellement ou à l’aide d’un programme informatique distinct.
La façon dont tout ceci se passe ne joue en fait aucun rôle; dans chacun des cas, c’est l’homme qui analyse le dessin du réseau de canalisations et qui arrive à la conclusion qu’une certaine partie de celui-ci doit être réalisé dans un diamètre donné.
L’homme de métier appliquera ensuite (parfois inconsciemment) un certain nombre de règles qu’il connaît, mais que le programme de dessin ignore.
Il sait qu’une cuvette de W.C. se caractérise par un certain diamètre de raccordement et qu’elle ne fonctionnera pas s’il la raccorde sur un diamètre insuffisant.
Il sait qu’à un branchement, le diamètre de la section d’évacuation doit être au moins égal à celui de la plus grande section d’arrivée.
Il sait quelle sorte de tuyau il va mettre en oeuvre et quels sont les diamètres disponibles.
Après avoir déterminé les diamètres en question, il pourra étoffer son schéma original (ligne simple) afin d’y incorporer le diamètre des différentes parties de l’installation (ligne double).
Alors qu’au début, seuls apparaissaient les axes des tuyauteries, les diamètres des différentes sections sont maintenant repris sur le plan.
Rien n’a vraiment changé pour l’ordinateur, seul le nombre de lignes a augmenté.
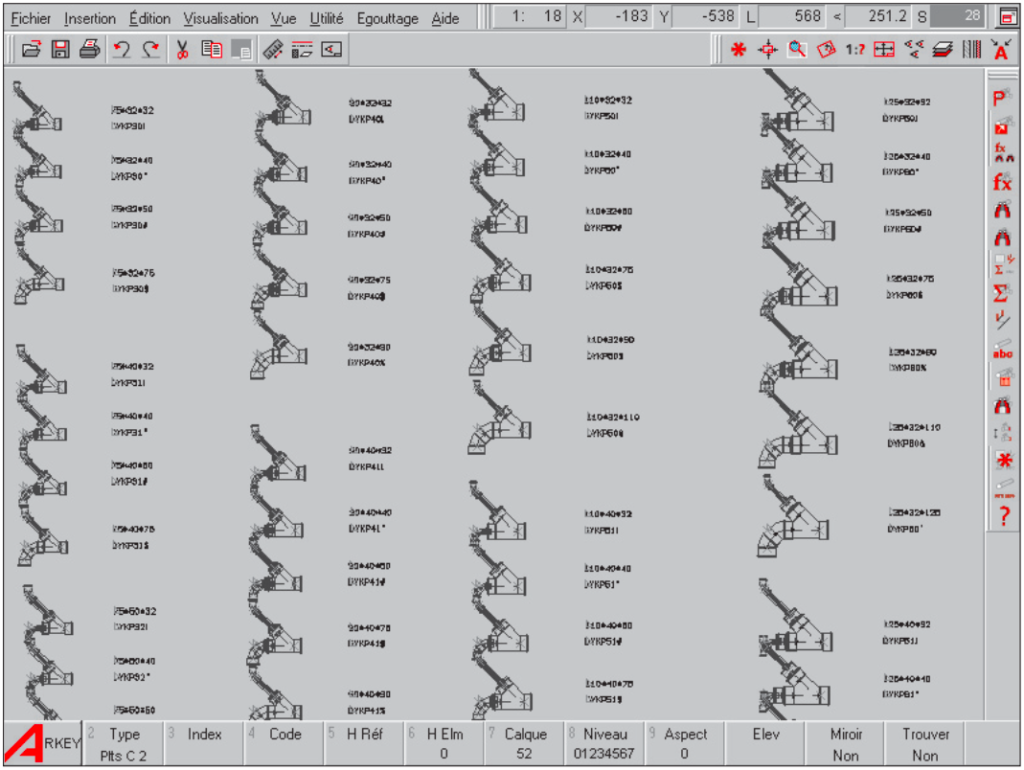
Vient maintenant pour le dessinateur l’ennuyeux travail de dessiner les accessoires de raccordement.
Pour ce faire, il dispose heureusement d’une bibliothèque dans laquelle sont repris tous les acces-soires correspondant au système choisi. Il cherche les éléments convenables dans la bibliothèque et les place aux bons endroits dans le plan de ses canalisations.
Il ne lui reste plus qu’à raccourcir les tuyaux au droit des accessoires (et donc les lignes qui représentent les conduites) et il a terminé.
Où réside le problème ? Le problème est que les différentes étapes de la réalisation ne sont possibles que grâce à l’intervention humaine. Un certains nombre de ces étapes intermédiaires se prêtent pourtant à merveille à une automatisation. Ceci n’est toutefois possible que si nous pouvons apprendre les concepts «appareil sanitaire», «section de conduite», «tuyau et diamètre» à l’ordinateur.
En ce qui concerne les accessoires, il ne suffit pas non plus qu’il existe une icône portant un nom donné, il nous faut aussi définir qu’à l’aide de cet accessoire, il est possible de réaliser un coude ou un raccord en T entre deux tuyaux d’un diamètre donné.
Ceci est plus difficile qu’il n’y paraît, car si un homme peut simplement dire qu’il est évident que cela ne correspond pas, il faudra bien faire comprendre d’une manière ou de l’autre ce qui va ou ne va pas à l’ordinateur.
Un ordinateur n’a pas d’yeux et ne voit donc rien.

II.7.3. PERTE D’IMPORTANCE DE LA REPRÉSENTATION

Comme un ordinateur ne peut rien voir, nous devons bien être conscients du fait que, pour lui, les lignes et le dessin sont secondaires.
Si nous parvenons à faire comprendre à l’ordinateur comment est constitué une tuyauterie, il sera à même de nous en donner une représentation.
Nous pourrons alors lui demander le dessin que nous voulons, en ligne simple, en ligne double, avec ou sans accessoire ou isométrique. L’homme commande, l’ordinateur exécute.
L’ordinateur peut donc dessiner quelque chose qu’il «comprend», mais il ne peut «comprendre» ce qui est dessiné.

Si nous revenons à notre exemple de la tuyauterie, quelles sont les implications de ce que nous venons de voir?
Il faut trouver une méthode qui, au sein du logiciel de CAD, permette de déterminer ce qu’est un appareil sanitaire, où il se trouve et quelles en sont les caractéristiques.

Les caractéristiques d’un appareil sanitaire raccordé à l’égout intérieur sont, par exemple:

• la capacité d’évacuation,
• le sens d’évacuation,
• le diamètre de raccordement.

La capacité d’évacuation indique le nombre de litres que l’appareil donné est capable d’évacuer par seconde.
Le sens d’évacuation est important, car il existe des cuvettes de W.C. à sortie par le bas ou par l’arrière.
Le diamètre de raccordement détermine le diamètre minimal de la canalisation sur laquelle le W.C. est raccordé (même si, par calcul, une canalisation de diamètre inférieur pourrait suffire).
On détermine ensuite le point de départ et d’arrivée de chacune des sections de conduite. Dans ce cas, les caractéristiques sont la somme calculée des capacités d’évacuation et, sur base de celle-ci, le diamètre intérieur minimal, exprimé en millimètres.
Pour chaque sorte de tuyau, il faudra enregistrer les diamètres extérieurs disponibles ainsi que les diamètres intérieurs correspondants.
Remarquons qu’une section de conduite et un tuyau sont deux choses différentes.
Une section de conduite doit présenter un diamètre intérieur requis.
Un tuyau possède un diamètre fixe, à choisir parmi tous les diamètres possibles. Un tuyau peut donc servir à une section de conduite, à condition que son diamètre intérieur soit égal ou supérieur au diamètre minimal de la conduite concernée. La section détermine la fonction (ici, l’évacuation d’une quantité donnée d’eau usée de A vers B) et le tuyau est le produit concret.
En ce qui concerne les accessoires, il faudra déterminer, pour chacun d’eux, le diamètre de l’évacuation ainsi que le sens et le diamètre de chacune des entrées.
Les accessoires permettent de raccorder des tuyaux et non des sections.
La détermination des accessoires à utiliser ne peut se faire que lorsque les tuyaux correspondant aux sections auront été sélectionnés.
Il faudra ensuite déterminer, pour chaque accessoire, de combien le tuyau doit être raccourci pour autoriser son montage.
L’accessoire est finalement placé au point concerné de la tuyauterie dans le sens de l’évacuation. Le seul élément qui manque encore est l’endroit où le réseau d’égout quitte le bâtiment. Cet élément est nécessaire afin de pouvoir établir si le réseau est complet.
Ce point de raccordement possède, comme tout autre appareil sanitaire, un diamètre de raccordement et un sens d’évacuation.

Chaque réseau peut être spécifié à l’aide de ces cinq caractéristiques différentes.

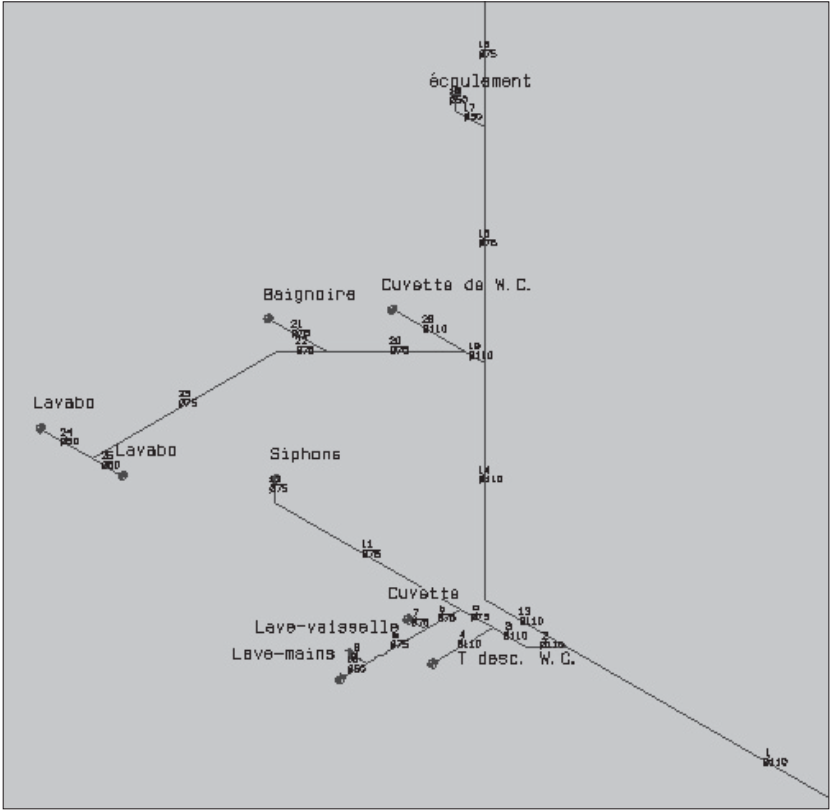
Le plus parlant est peut-être de se représenter un arbre dont:

• les appareils sanitaires sont les feuilles;
• les sections de conduite sont les branches;
• la descente est le tronc et le point de raccordement à l’égout extérieur correspond aux racines.

Les branches se ramifient en tuyaux et, à chaque embranchement, prend place un accessoire.
Insistons encore une fois sur le fait que les lignes ne sont pas déterminantes lors de l’élaboration du dessin.
Il est évident qu’à chaque élément on fait aussi correspondre un dessin, ce qui permet de dessiner le réseau. Mais la signification du réseau ne dépend cependant pas de ce dessin.
Si tous les dessins venaient à être effacés, on saurait toujours ce qui est un appareil sanitaire et ce qui est une section de conduite.
Seule l’introduction des données serait plus difficile car la personne réalisant ce travail ne verrait plus ce qu’elle fait.

II.7.4. CALCUL AUTOMATIQUE DES DIAMÈTRES

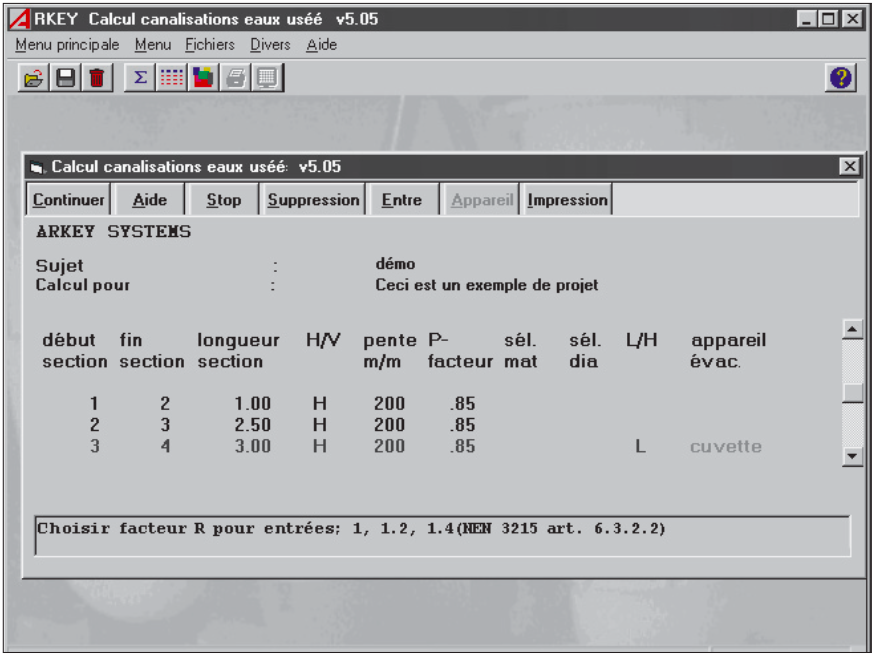
Pourquoi se donner tant de mal?

Les avantages du système deviennent cependant rapidement évidents.

Prenons, par exemple, la détermination des diamètres des tuyaux des différentes sections.

Quand le dessinateur a placé les appareils sanitaires et indiqué les sections de conduite désirées (cela ressemble à du dessin, mais nous savons qu’il s’agit de plus que cela), le logiciel peut, même sans calcul, poser une hypothèse sur la base du diamètre de raccordement.
Nous avons vu plus haut que la règle de base était que le diamètre d’une section de raccordement ne pouvait jamais être inférieur à celui du raccordement de l’appareil sanitaire.
De même, le diamètre de l’évacuation d’un point déterminé ne peut jamais être inférieur à celui de la plus grande arrivée. Sur base de ces deux règles, le logiciel de CAD peut calculer le diamètre des tuyaux de chaque section puisque toutes les données sont connues.
En réalité, les possibilités sont encore plus étendues.
Toutes les données permettant de calculer les diamètres sont connues. La transmission de ces données au programme de calcul permettra de déterminer le diamètre intérieur minimal de chaque section.
Il sera ensuite possible de déterminer de manière automatique le diamètre des tuyaux correspondants.

II.7.5. CALCUL DES COÛTS ET PRÉPARATION DU TRAVAIL

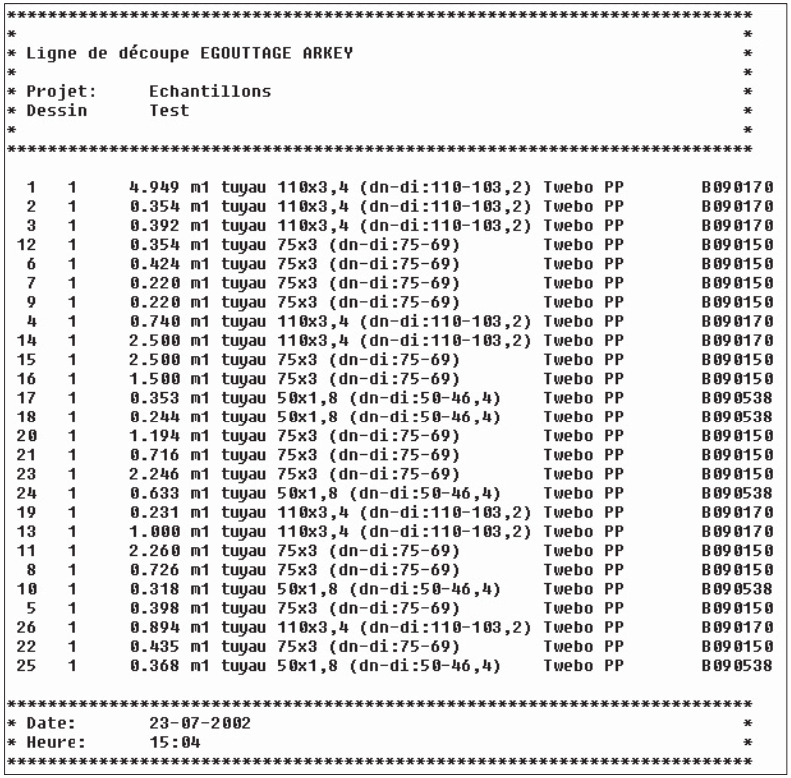
Il est évident qu’une fois la tuyauterie entièrement connue, il est possible d’extraire un métré quantitatif complet et fiable.

Si les prix unitaires et les heures de main-d’œuvre sont couplés aux différents éléments, il devient également possible de calculer les coûts.

Ces données peuvent, en outre, être utilisées pour préparer le travail.

On peut se baser sur le métré quantitatif pour commander les matériaux et, comme les longueurs des tuyaux sont connues au millimètre près, elles peuvent servir en cas de préfabrication.

II.8. PRATIQUE DE LA CONCEPTION PAR ORDINATEUR

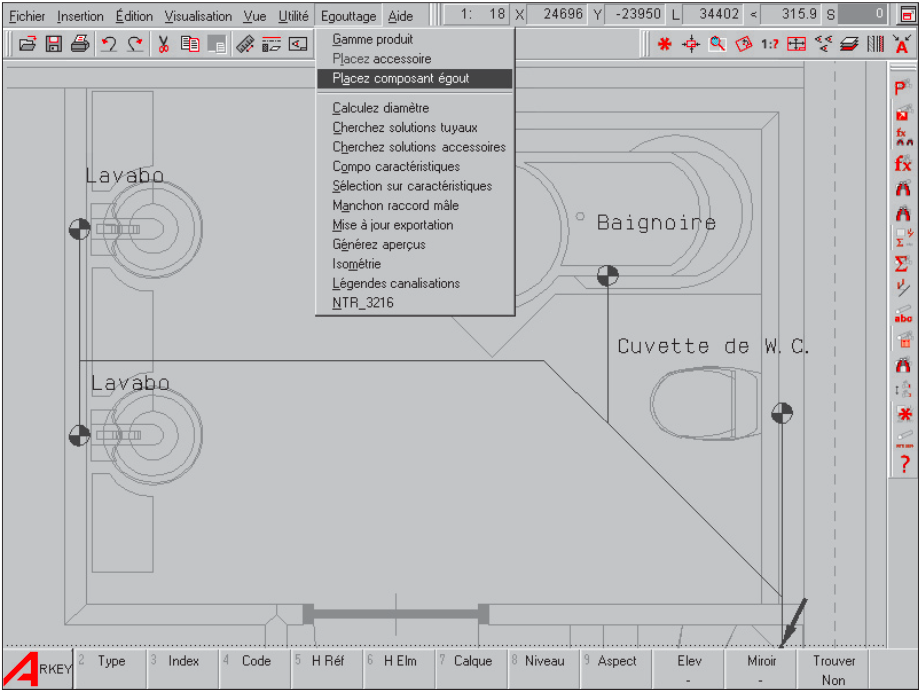
Le projet d’un réseau d’égout se déroule selon les étapes suivantes:

II.8.1. DESSIN DE LA TUYAUTERIE

La tuyauterie est dessinée sur base d’un plan de construction placé en arrière-plan.

II.8.1.1. Appareils d’évacuation

L’emplacement exact du raccordement au réseau d’égout des appareils d’évacuation, tels que la baignoire, le W.C. ou le lavabo, doit figurer sur ce dessin.

Dans le cas d’un lavabo, ce sera par exemple l’endroit où le siphon se raccorde au tuyau d’évacuation dans le mur ou dans le sol.

Ces appareils d’évacuation se sélectionnent dans une bibliothèque. Cette dernière contient une collection de différents appareils d’évacuation prédéfinis. Chacun de ces appareils d’évacuation est associé à ses caractéristiques d’évacuation, telles que le volume d’écoulement de base ou le diamètre de raccordement nominal ou réduit.

Ainsi, l’appareil d’évacuation «Baignoire» est-il associé à un volume d’écoulement = 1 l/s, à un diamètre de raccordement nominal = 57 mm et à un diamètre de raccordement réduit = 44 mm.

II.8.1.2. Extrémité du réseau

On indique ensuite l’emplacement où la tuyauterie se termine.

En pratique, il s’agit souvent de l’endroit où le réseau local se branche sur le réseau d’égout communal.

II.8.1.3. Canalisations

Enfin, les canalisations d’égout sont dessinées à l’aide de lignes verticales et horizontales qui se raccordent entre elles. Chacune de ces lignes matérialise l’axe des tuyaux.

A ce moment, on ne connaît encore ni le diamètre du tuyau, ni le matériau dont il sera constitué.

Un réseau de conduites est entièrement dessiné quand un tuyau (ligne) débute auprès de chaque appareil d’évacuation et rejoint indirectement, via d’autres conduites, l’extrémité du réseau.

Il est possible de demander au programme une vue isométrique 3D des tuyauteries, afin de vérifier visuellement si la tuyauterie dessinée est correcte et complète.

II.8.2. CALCUL DES DIAMÈTRES MINIMUM DES CONDUITES

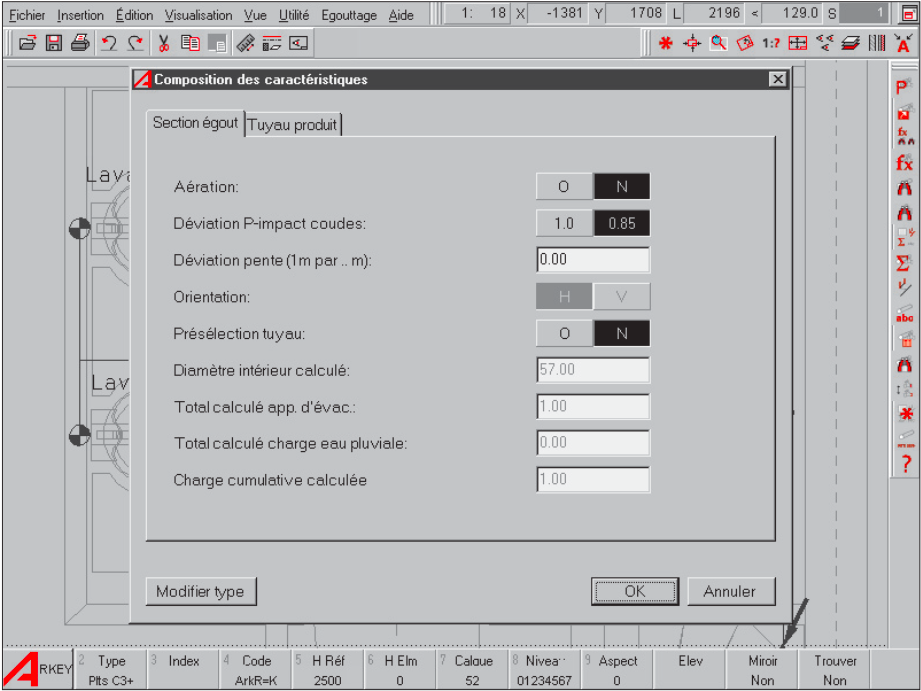
Maintenant que la tuyauterie est dessinée, il est possible de calculer automatiquement les diamètres intérieurs minimum requis.
Ce calcul se base sur les normes et les directives en vigueur dans la pratique, telles que la norme hollandaise NEN 3215 et la directive pratique NPR 3216.
Le calcul est effectué sur la tuyauterie dessinée. Il tient compte des longueurs et de la position des conduites (horizontale ou verticale) ainsi que de l’emplacement et de la capacité d’évacuation requise des appareils.
Il tient également compte d’autres paramètres, tels que la pente nécessaire des conduites ainsi que la manière dont le réseau sera utilisé (dans une maison ou une construction non résidentielle). Toutes ces données sont déduites automatiquement de la tuyauterie dessinée et sont transmises au programme de calcul.
Le programme de calcul signale l’introduction de configurations erronées. Les résultats du calcul comprennent, entre autres, la capacité d’évacuation totale en l/s de chaque conduite ainsi que le diamètre intérieur minimum requis.

II.8.3. SÉLECTION AUTOMATIQUE DU DIAMÈTRE OPTIMAL DES TUYAUX

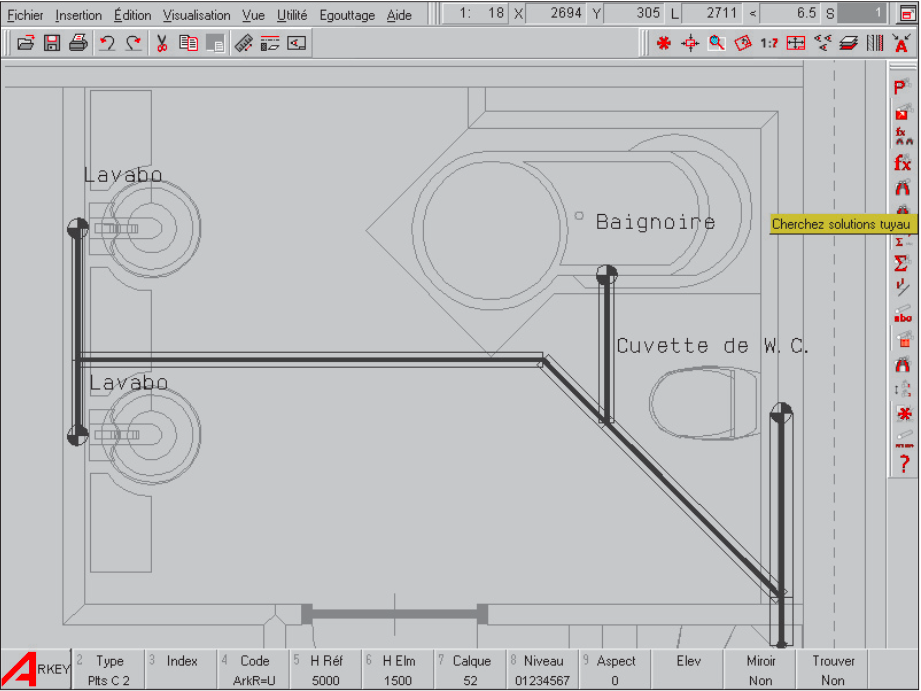
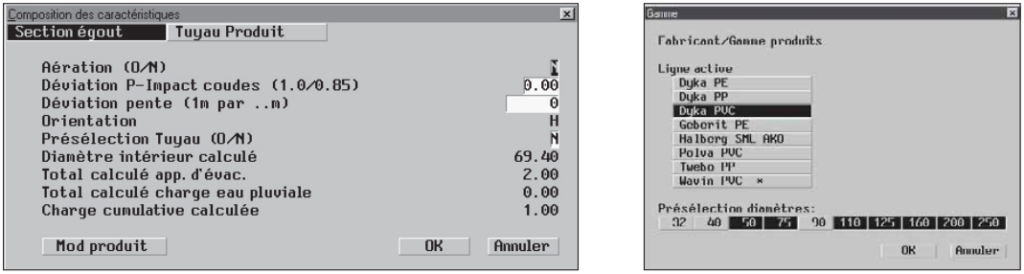
On sélectionne ensuite la ligne de produit utilisée pour les sections de conduite, ce qui permet de connaître les caractéristiques du matériau (p.ex. PVC, PE ou PP).

Les diamètres minimum des sections de conduite sont ensuite calculés selon NEN 3215 et NPR 3216.

Le tracé de la tuyauterie dessinée, l’emplacement et la capacité requise des appareils sont automatiquement déduits du dessin et transmis au programme de calcul.
La connaissance (par calcul) des diamètres minimum des tuyaux et la sélection de la ligne de produits souhaitée pour les sections de conduite permettent de rechercher automatiquement les tuyaux correspondants.
L’utilisateur peut spécifier quels diamètres il ne souhaite pas mettre en oeuvre (p.ex. ne pas utiliser le diamètre 90 mm).
Il existe en outre une possibilité de modifier ultérieurement le diamètre d’un tuyau (p.ex. remplacer un diamètre de 75 mm par un de 110 mm).

II.8.4. PLACEMENT AUTOMATIQUE DES ACCESSOIRES

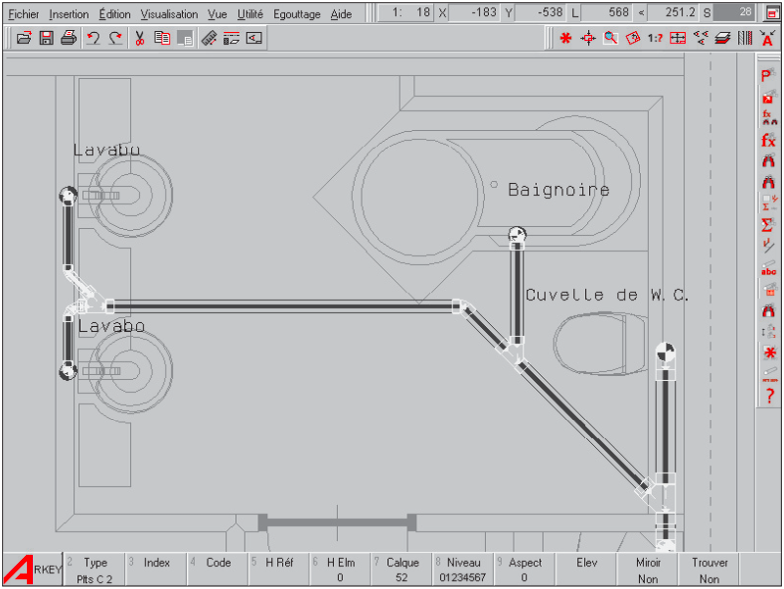
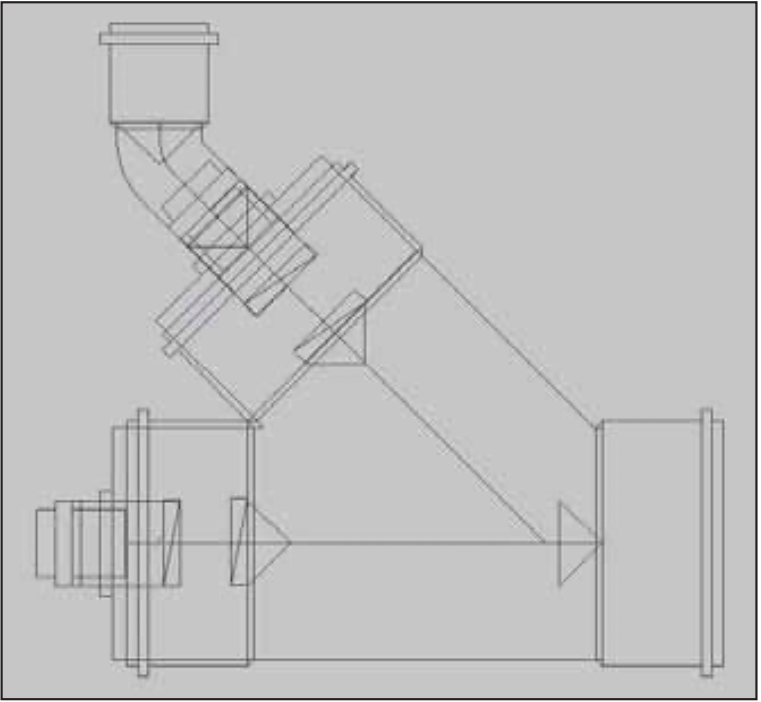
Au moment où un tuyau a été sélectionné pour chaque section de conduite, il est possible d’ajouter automatiquement les accessoires.
Ceci s’effectue automatiquement à l’aide d’une fonction qui tient compte des diamètres calculés des sections de conduite, de la ligne de produits et de la façon dont les sections se raccordent (p.ex. selon un coude à 45 degrés de 75 mm ou un T à 90 degrés de 110 et de 75 mm).
La longueur des sections est automatiquement adaptée en fonction de la profondeur d’emboîtement de chacun des accessoires. Un problème de branchement peut être résolu à l’aide de plusieurs accessoires. Par exemple, un branchement en T de 90 degrés peut être réalisé par un T de 45 degrés suivi d’un coude de 45 degrés.
Un autre exemple est constitué par un accessoire muni d’un anneau de réduction. Il est en outre possible de modifier ou d’ajouter manuellement des accessoires. Ici encore, la longueur des sections sera adaptée automatiquement aux profondeurs d’emboîtement modifiées.

II.8.5. RÉALISATION DE LA TUYAUTERIE

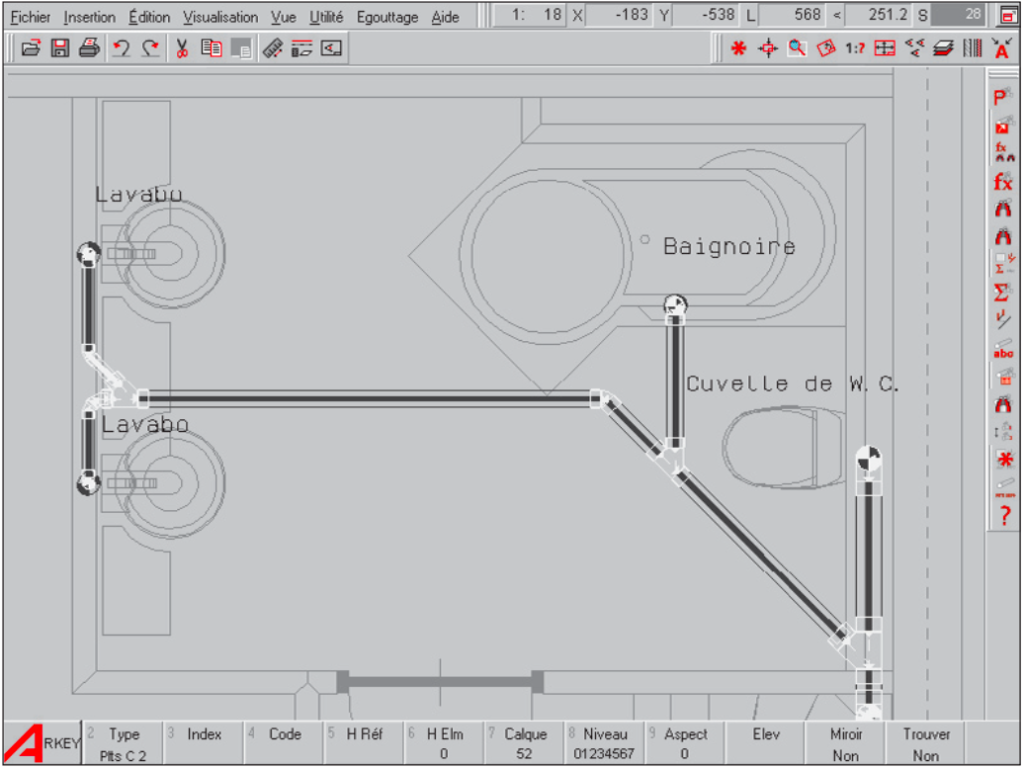
Le projet est prêt une fois que la tuyauterie est réalisée à l’aide de produits concrets.

Les données peuvent ensuite être réutilisées dans la suite du processus de fabrication.

Il est possible d’extraire des listes de sciage précises en vue de la préfabrication.

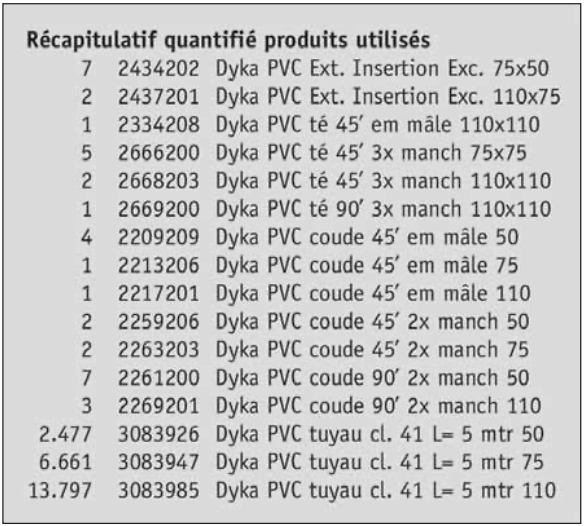
On peut également générer des relevés des produits utilisés à l’attention de l’administration des stocks, des achats ou de l’interface avec d’autres logiciels de calcul.

Outre une impression de la tuyauterie dessinée, dans laquelle sont automatiquement insérés les textes reprenant les caractéristiques des tuyaux (comme la longueur, le diamètre, le numéro de la section), il est aussi possible de réaliser automatiquement une vue isométrique ou un récapitulatif textuel de la tuyauterie.

Au sommaire

MODULE II – DESSIN: LECTURE DE PLANS

II.1. AVANT-PROPOS
II.2. DESSIN DE CONSTRUCTIONS GÉOMÉTRIQUES
II.2.1. Perpendiculaires
II.2.1.1. Perpendiculaire au milieu d’un segment de droite [AB]
II.2.1.2. Perpendiculaire en un point donné d’une droite a
II.2.1.3. Perpendiculaire à l’extrémité d’un segment de droite [AB], méthode 1
II.2.1.4. Perpendiculaire à l’extrémité d’un segment de droite [AB], méthode 2
II.2.1.5. Perpendiculaire à une droite a à partir d’un point P
II.2.2. Parallèles
II.2.2.1. Parallèle à une distance donnée, par exemple 18 mm
II.2.2.2. Parallèle passant par un point donné P
II.2.3. Divisions
II.2.3.1. Diviser un segment de droite [AB] en n parties égales (p.ex. 5), méthode 1
II.2.3.2. Diviser un segment de droite [AB] en n parties égales (p.ex. 5), méthode 2
II.2.3.3. Division des angles
II.2.4. Tangentes et polygones réguliers
II.2.4.1. Tangente à un cercle à partir d’un point P
II.2.4.2. Triangle régulier inscrit dans un cercle
II.2.4.3. Quadrangle régulier inscrit dans un cercle
II.2.4.4. Hexagone régulier inscrit dans un cercle
II.3. REPRÉSENTATION DES SYMBOLES SANITAIRES
II.4. LECTURE DE PLANS (plans en annexe)
II.5. DESSIN ISOMÉTRIQUE
II.5.1. Conventions
II.5.2. Dessin des symboles
II.5.3. Cotation
II.5.4. Coudes à 90°
II.5.5. Coudes non à 90° dans un même plan
II.5.6. Coudes non à 90° dans deux plans
II.5.7. Cas particuliers
II.5.8. Applications
II.5.9. Exemple d’installation
II.6. CROQUIS
II.7 DESSIN FONCTIONNEL SUR ORDINATEUR
II.7.1. Du dessin à la signalisation
II.7.1.1. Historique
II.7.1.2. Dissociation concepteur-exécutant
II.7.1.3. Le dessin en tant que document
II.7.1.4. Conventions uniformes
II.7.2. Evolution
II.7.2.1. Du crayon électronique
II.7.2.2. … via les icônes
II.7.2.3. … et les applications
II.7.2.4. … vers une nouvelle génération de systèmes CAD
II.7.3. Perte d’importance de la représentation
II.7.4. Calcul automatique des diamètres
II.7.5. Calcul des coûts et préparation du travail
II.8. PRATIQUE DE LA CONCEPTION PAR ORDINATEUR
II.8.1. Dessin de la tuyauterie
II.8.1.1. Appareils d’évacuation
II.8.1.2. Extrémité du réseau
II.8.1.3. Canalisations
II.8.2. Calcul des diamètres minimum des conduites
II.8.3. Sélection automatique du diamètre optimal des tuyaux
II.8.4. Placement automatique des accessoires
II.8.5. Réalisation de la tuyauterie