Table of Contents
1.1 Introduction
En génie mécanique comme dans d’autres sciences, le choix d’un modèle associé à un phénomène relève du domaine de l’art de l’ingénieur. Il suppose une parfaite connaissance des disciplines scientifiques et surtout une grande accoutumance au réel. Le choix d’une schématisation complexe impliquant un traitement numérique, souvent long et coûteux, n’est pas toujours adapté.
De nombreuses pièces du génie mécanique relèvent de modélisations plus simples, susceptibles de développements analytiques avec une concordance suffisante entre les résultats théoriques et expérimentaux. Une illustration de ces propos est constituée par la notion de poutre associée à des pièces dont la dimension dans une direction est plus importante que dans les deux autres. Des hypothèses spécifiques entraîneront des simplifications notables par rapport au problème tridimensionnel sans trop altérer les résultats. Par exemple, l’axe d’une broche de machine-outil peut être considéré comme une poutre dont les liaisons avec le bâti sont conditionnées par les roulements utilisés et leurs montages. Cette modélisation est légitime, car la longueur de la broche dans la direction de l’axe de rotation est grande vis à vis de ses dimensions transversales.
La Résistance des Matériaux (que nous désignerons maintenant par RdM ) est la science du dimensionnement. Elle est issue d’une théorie plus générale, la Mécanique des Milieux Continus, qui permet de concevoir une pièce mécanique, un ouvrage d’art ou tout objet utilitaire, c’est à dire d’abord imaginer les formes et le squelette géométrique qui remplissent les fonctions demandées ; et ensuite déterminer les quantités de matière nécessaires et suffisantes pour réaliser ces formes en assurant une résistance sans dommage de l’objet à tous les efforts auxquels il sera soumis pendant son service. Ce dimensionnement fait appel à des calculs qui prévoient le comportement de l’objet dont la conception doit réunir les meilleures conditions de sécurité, d’économie et d’esthétique.
1.2 Un peu d’histoire
Les premières recherches scientifiques connues sur la résistance d’éléments de construction ne remontent qu’à la fin du XVeme siècle avec les travaux de Galilée sur la tension et la flexion des poutres. Il ne semble pas que les constructions anciennes aient fait l’objet d’études prévisionnelles concernant la résistance. Bien évidemment, les constructions qui se sont effondrées ne sont plus présentes actuellement ! La cathédrale de Prague, par exemple, s’est effondrée six fois avant que son architecte soit le seul à accepter de mettre le feu aux échafaudages pour vérifier la tenue de la septième construction : c’est actuellement un bijou.
L’absence de souci d’économie de matière, le sens élevé de l’esthétique (une forme esthétique est souvent une forme optimale vis-à-vis de la résistance), des connaissances empiriques ont permis la réalisation d’ouvrages durables. En 1678, Robert Hooke énonce les bases de la théorie de l’élasticité linéaire (réversibilité et proportionnalité des déformations par rapport aux efforts), qui rend compte des petites déformations de la plupart des corps solides. Elle est utilisée peu après par Edme Mariotte et Jean Bernoulli pour résoudre des problèmes de flexion de poutres. Après les travaux de Charles Augustin Coulomb, Henri Navier, Augustin-Louis Cauchy, entre autres, au milieu du XIXeme siècle, la résistance des matériaux est créée en

tant que science appliquée. Son développement rapide, dû aux travaux des ingénieurs du XXeme siècle, a conduit à l’élaboration de nombreuses méthodes de calcul analytique qui ont pu être érigées en règles ou règlements à l’usage des bureaux d’étude. L’avènement des ordinateurs a rendu possible l’exploitation de méthodes numériques générales qui permettent de résoudre les problèmes posés par les structures complexes (assemblages de poutres, plaques). Les recherches sont, depuis les années 1970, orientées vers le développement de ces méthodes, vers l’étude des petites et grandes déformations permanentes des matériaux, des phénomènes de rupture, de la résistance aux environnements complexes (efforts évolutifs, hautes et basses températures) et vers l’utilisation de matériaux nouveaux (superalliages, polymères, matériaux composites, céramiques).
1.3 Le solide étudié
La RdM est une théorie simplifiée qui nécessite de ne s’intéresser qu’à des solides particuliers, considérés ici comme déformables. Ainsi un certain nombre de restrictions sont nécessaire pour pouvoir utiliser la RdM. Ces restrictions portent sur la géométrie du solide étudié, le matériau dont il est constitué, et dans une moindre mesure les liaisons et les efforts extérieurs. Nous allons donc détailler chacun de ces points.
1.3.1 Définition générale
Une poutre est un solide engendré par une surface plane (S) dont le centre d’inertie géométrique G décrit une courbe G0G1, le plan de (S) restant normal à la courbe G0G1 (Fig 1.2). Le centre d’inertie peut dans de nombreux cas être confondu avec le centre de gravité. Nous avons supposé l’aire (S) constante ; la poutre est alors dite de section constante. Mais très souvent, en vue de proportionner les dimensions de la poutre aux efforts qu’elle doit supporter, l’aire (S) varie lorsque son centre de gravité décrit la fibre moyenne ; la poutre est alors dite de section variable, et l’on supposera que la section varie continuement le long de la fibre neutre.
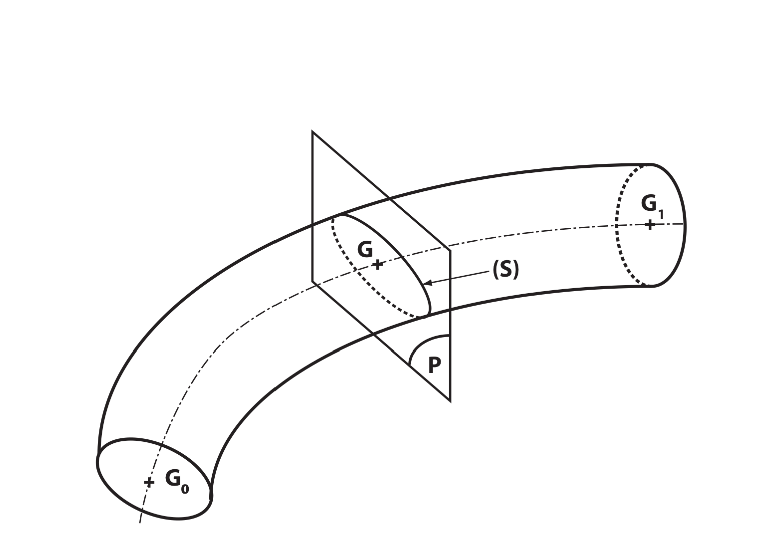
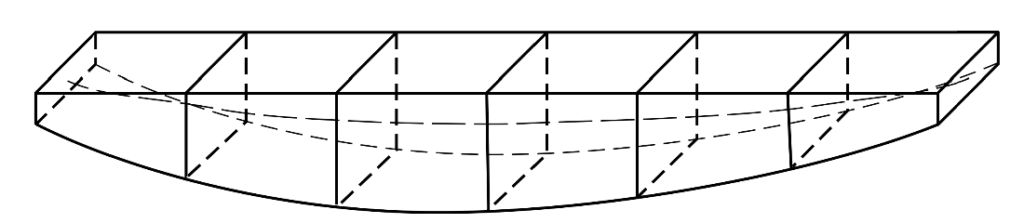
Fig61 Exemples de géométries « poutre »
ples de géo)
L’aire (S) est appelée section droite de la poutre. La courbe G0G1 est appelée fibre moyenne de la poutre. Le volume engendré le long de G0G1 par un petit élément dS de la surface (S) porte le nom de fibre ; cette définition n’a, bien entendu, aucun rapport avec la structure de la matière. Une poutre gauche est une poutre dont la fibre moyenne est une courbe gauche ; une poutre plane est une poutre dont la fibre moyenne est une courbe plane ; une poutre droite est une poutre dont la fibre moyenne est un segment de droite orienté. Une poutre à plan moyen est une poutre plane dont un plan de la fibre moyenne est un plan de symétrie, appelé plan moyen, de la poutre.
Il faut de plus que certaines propriétés de la géométrie soit vérifiée :
- le rayon de courbure de la ligne moyenne est grand par rapport à la plus grande dimension transversale de la section droite (rapport supérieur à 5)
- la longueur de la ligne moyenne est grande par rapport à la plus grande dimension transversale de la section droite (rapport supérieur à 5)
Dans le cas des poutres droites, le rayon de courbure étant infini, la première propriété est naturellement vérifiée.
La poutre étant amenée à se déformer, on va de plus supposer que les déformations subies par la poutre ainsi que les déplacements qui peuvent être mesurés, restent petits. En effet, les déformations doivent rester petites pour que le reste dans le domaine élastique, et les déplacement doivent rester petits pour que les points d’application des efforts extérieurs ne soient pas modifiés. On pourra ainsi utiliser les efforts calculés en statique (donc calculés en supposant que les solides sont indéformables) pour faire une étude de déformation de la poutre. Typiquement, on supposera que les déplacements restent inférieurs au centième de la longueur de la ligne moyenne. On dira alors que l’on travaille dans l’hypothèse de petits-déplacements encore appelée hypothèse des petites perturbations (ou encore H.P.P.).
1.3.2 Restriction au cas des poutres droites à plan moyen
Dans le cadre de ce cours, nous ne nous intéresserons qu’aux poutres droites à plan moyen (voir Fig. 1.4). Ainsi, une poutre est maintenant totalement définie par sa fibre moyenne et par sa section droite. Pour les poutres à section variable, il faut aussi se donner la forme de l’évolution le long de la fibre moyenne.
La fibre moyenne est un segment de droite qui est défini par une origine et par une extrémité. On peut donc orienter la fibre moyenne et associer à la poutre un repère (0,−→x , −→y , −→z ). Traditionnellement :
- le vecteur −→x est le vecteur unitaire de la fibre moyenne,−→y est tel que le plan (
- →x , −→y ) est le plan de symétrie ou plan moyen,
- le vecteur −→z est choisi de tel sorte que le repère (0,
- →x , −→y , −→z ) soit direct (Fig.1.5),
- le point O est positionné à l’origine de la fibre moyenne. Pour décrire la poutre on peut donc la représenter par sa ligne moyenne et sa section droite (figure 1.5).
1.4 Hypothèses sur le matériau
Pour toutes les études que nous mènerons en RdM, nous allons considérer que le matériau dont est constitué la poutre est un matériau :
Au sommaire
Introduction
1 Hypothèses de la Résistance des Matériaux
- 1.1 Introduction
- 1.2 Un peu d’histoire
- 1.3 Le solide étudié
- 1.3.1 Définition générales
- 1.3.2 Restriction au cas des poutres droites à plan moyen s
- 1.4 Hypothèses sur le matériaus
- 1.4.1 Homogénéités
- 1.4.2 Isotropies
- 1.4.3 Élasticité linéaires
- 1.5 Hypothèses fondamentales de la RdMs
- 1.5.1 Principe de Saint-Venant et conséquences
- 1.5.2 Hypothèse de Navier-Bernoulli
- 1.6 Conditions aux limites
- 1.6.1 Efforts extérieurs
- 1.6.2 Liaisons
- 1.7 Ce qu’il faut retenir
2 Torseur des efforts intérieurs – Notion de contrainte
- 2.1 Introduction
- 2.2 Torseur des efforts intérieurs
- 2.2.1 Bilan et règles de calcul
- 2.2.2 Exemple
- 2.3 Dénomination des composantes et des sollicitations associées
- 2.4 Diagrammes
- 2.5 Notion de contrainte – Vecteur contrainte
- 2.5.1 Contraintes normale et tangentielle
- 2.5.2 Intérêt
- 2.6 Ce qu’il faut retenir
3 Sollicitation élémentaire : la traction
- 3.1 Définition
- 3.2 Relation contrainte/effort normal
- 3.3 L’essai de traction
- 3.4 Relation contrainte/déformation
- 3.5 Relation déformation/déplacement
- 3.6 Critère de dimensionnement
- 3.7 Bilan des relations entre grandeurs globales et locales
- 3.8 Ce qu’il faut retenir
4 Sollicitation élémentaire : la torsion
- 4.1 Hypothèse complémentaire
- 4.2 Définition
- 4.3 Relation contrainte/moment de torsion
- 4.4 Relation contrainte/déformation
- 4.5 Relation déformation/rotation
- 4.6 Critère de dimensionnement
- 4.7 Bilan des relations entre grandeurs globales et locales
- 4.8 Ce qu’il faut retenir
5 Sollicitation élémentaire : la flexion
- 5.1 Définition
- 5.2 Relation effort tranchant/moment fléchissant
- 5.3 Relation contrainte normale/moment fléchissant
- 5.4 Équation de la déformée
- 5.5 Contraintes tangentielles
- 5.6 Ordre de grandeur des contraintes
- 5.7 Critère de dimensionnement
- 5.8 Bilan des relations entre grandeurs globales et locales
- 5.9 Ce qu’il faut retenir
6 Concentration de contraintes
- 6.1 Introduction
- 6.2 Mise en évidence
- 6.3 Coefficient de concentration de contraintes
- 6.4 Abaques, formules approchées et logiciels
- 6.5 Ce qu’il faut retenir
7 Le flambage
- 7.1 Introduction
- 7.2 Flambage d’Euler
- 7.3 Dimensionnement
- 7.4 Ce qu’il faut retenir

1 Commentaire
salut