Table of Contents
1-Introduction
Un des mouvements les plus importants observés dans la nature est le mouvement oscillatoire, en particulier le mouvement harmonique : oscillations d’un pendule, d’une masse attachée à un ressort, d’un gratte-ciel, etc.
Dans le cas des oscillations de systèmes mécaniques conservatifs isolés, on parle d’oscillations libres ; en présence de frottement, l’amplitude des oscillations décroît et on observe des oscillations amorties. Si les oscillations sont entretenues par une action extérieure, on parle d’oscillations forcées. Dans ce dernier cas, on verra apparaître de nouveaux phénomènes tels que la résonance, qui peut avoir des conséquences catastrophiques. Cependant, la plupart des problèmes observés (mis
à part les tremblements de terre) sont liés à des critères d’aptitude au service. Ceux-ci demandent une connaissance précise du comportement linéaire des structures
2-Notions de base
2.1 Mouvements
Une structure sollicitée par une charge subit un certain mouvement ; dans le cas d’une sollicitation uniquement en traction, le mouvement sera translationnel et, dans le cas d’une flexion, celle-ci imprimera à la structure un mouvement translationnel et rotationnel.
Le mouvement oscillatoire d’une structure, dont le lieu géométrique est connu (dans un système de coordonnées déterminé) est caractérisé par un régime oscillatoire dépendant de la rigidité, de la masse et de l’amortissement de la structure. Les différents types de régime d’un mouvement oscillatoire sont le régime harmonique, le régime périodique et le régime transitoire.
Régime harmonique : décrit un mouvement oscillatoire au voisinage d’une position d’équilibre stable (ex. machinerie).
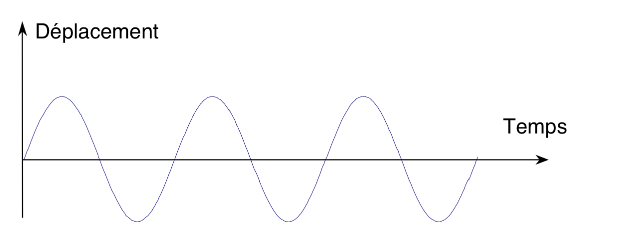
Régime périodique : décrit le même mouvement de manière périodique (ex. un piéton sur une passerelle).
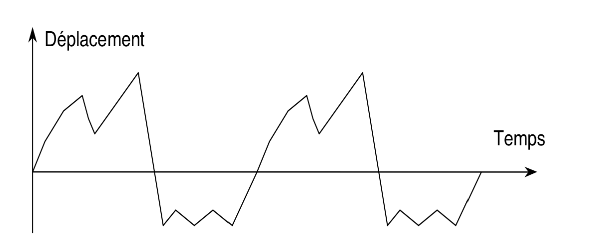
Transitoire : décrit un mouvement à caractère aléatoire (ex. trafic, séisme)
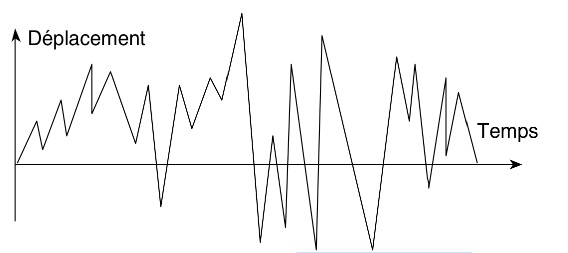
2.2 Evolution dans l’espace
Comme pour l’analyse statique, l’analyse dynamique des structures peut être effectuée dans le plan ou en trois dimensions. Ce cours se limitera à l’analyse des mouvements dans le plan. (Exemples : flexion plane, traction plane, etc.)
Mouvement dans le plan 3 degrés de liberté :
- translations selon x et y
- rotation autour de z (dans le plan xy)
Mouvement dans trois dimensions 6 degrés de liberté :
- translations selon x, y et z
- rotations autour de x, y et z
2.3 Définition de quelques grandeurs dynamiques
Pulsation propre :
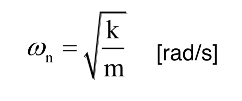
où
k : rigidité de l’élément [N/m]
m : masse de l’élément [kg]
Période propre :
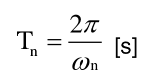
Fréquence ou fréquence propre:
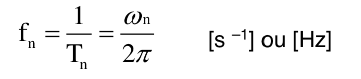
Remarque : Ces trois grandeurs (pulsation, période et fréquence) portent la dénomination « propre » car il s’agit de propriétés qui sont propres à l’oscillateur, dépendant uniquement de la masse et de la rigidité de celui-ci.
2.4 Rigidité de la structure
La rigidité d’une structure, k (en [N/m]), dépend des dimensions géométriques de celle-ci et du module d’élasticité du matériau qui la compose. La rigidité équivaut à la force qu’il faut exercer sur l’élément pour induire un déplacement unitaire. Il est à noter que ce cours se limite à l’utilisation de matériaux élastiques linéaires, la rigidité est donc constante tout au long des analyses. La rigidité vaut :
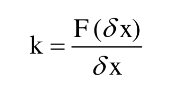
où :
x est un déplacement (translation / rotation) unitaire
F(x) est la force qui permet d’induire le déplacement unitaire x
Exemple 2.1- Rigidité d’un système à un degré de liberté
Voici l’exemple d’une colonne encastrée à la base dont une masse ponctuelle est fixée à son autre extrémité.
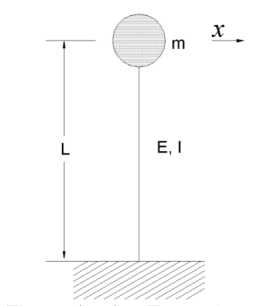
La rigidité de cette structure pour un déplacement horizontal de la masse prend la valeur suivante :
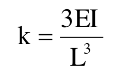
2.5 Rigidité équivalente d’un système
Dans le cas d’un système, une rigidité équivalente est définie. Pour plus d’informations, se référer aux cours de mécanique des structures et solides IV et V.
Système (de ressorts) en série :
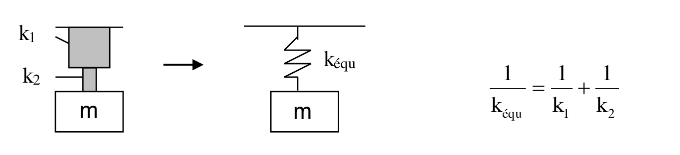
Système (de ressorts) en parallèle:
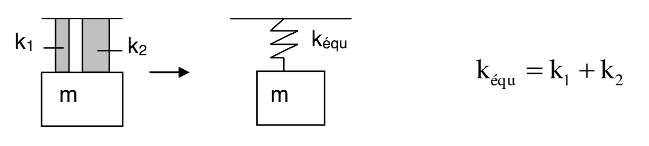
3.Systèmes à un degré de liberté
3.1 Oscillations non amorties
On parle d’oscillations non amorties quand l’amortissement est nul, c’est-à-dire c=0.
Avec
c : constante d’amortissement [Ns/m] ou [kg/s]
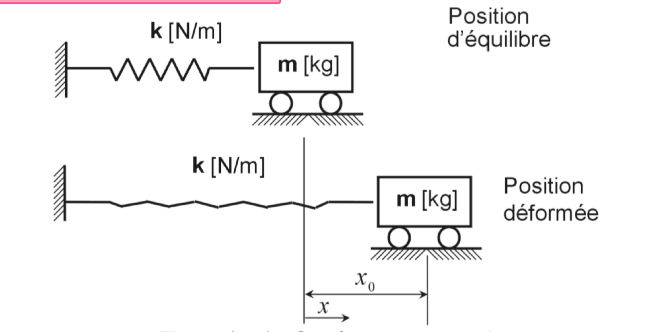
Schéma du système :
Un système non amorti peut être modélisé, à sa position d’équilibre et à sa position déformée, comme présenté à la figure (3.1). Les 5 hypothèses de base du modèle sont :
- le ressort a un comportement force/déformation qui est linéaire ;
- le ressort est sans masse ;
- il n’y a aucune friction provenant des rouleaux ;
- la masse est indéformable, et ;
- la résistance de l’air est négligée.
Remarque : En réalité, dans les applications du génie civil, ces hypothèses ne sont jamais satisfaites. Toutefois, l’utilisation d’un tel modèle est très utile car elle permet de saisir les interrelations entre les différentes grandeurs du système ainsi que les tendances associées.
Dans un système linéaire, la gravité n’a aucun effet sur le mouvement oscillatoire, même pour des oscillations verticales.