De manière générale, le rattachement est l’établissement de liens géométriques entre deux réseaux de points dont l’un sert de référence, afin d’exprimer l’autre dans la même référence géométrique que le premier ; notamment, il consiste à déterminer les coordonnées d’un point proche du repère connu, qui présente de plus grandes facilités d’utilisation ou de meilleures chances de conservation.
Les coordonnées du point rattaché M sont calculées à partir de celles du repère R (Fig. 9.20) par conversion P→R→
(fig. 9.20) par conversion P→R du vecteur RM après détermination des deux paramèters du rattachement : le gisement
GRM et la distance RM réduite au système de projection.
Si le repère R est stationnable, terasse ou château d’eau par exemple, effectuer un tour d’horizon sur un ou plusieurs points connus en coordonnées: A,B, etc. ainsi que sur le point rattaché M et mesurer la distance RM.
Le G0 de la station donne GRM , d’où les coordonnées de M.
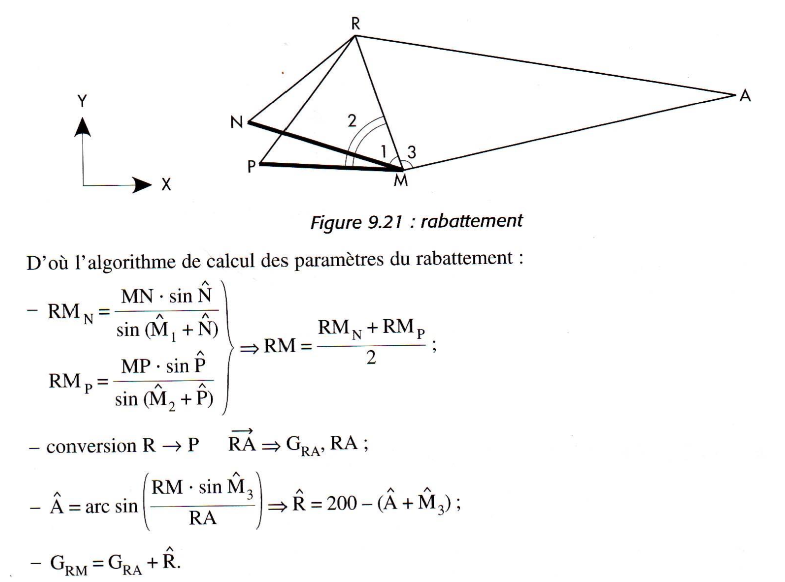
Si R est inaccessible, flèche de clocher à rabattre au sol par exemple (fig. 9.21), implanter M de manière à pouvoir viser, outre R, au moins un point connu A, et déterminer deux triangles RMN et RMP les plus équilatéraux possibles ; mesurer les distances MN et MP ainsi que tous les angles en M, N, P.
CHANGEMENT DE REPÈRE ORTHONORMÉ
Angle des repères
Le changement de repère orthonormé, composition d’un changement de base et d’une translation de l’origine, consiste à calculer dans un nouveau repère, appelé système général ou système national, les coordonnées de n points connus dans un ancien repère, appelé système local.
Dans tout ce qui suit, le nouveau repère est désigné par les lettres majuscules X, Y, l’ancien repère par les letters minuscules x, y (fig. 9.22).
Les deux applications topographiques potentielles du changement de repère orthonormé sont:
- le calcul dans le système de représentation plane Lambert par exemple, sans changement d’échelle, des sommets d’un canevas d’ensemble calculé dans un système Local orthonormé, sommairement orienté, à origine arbitraire ;
- le calcul des coordonnées, dans le système Lambert, de points de détail levés par abscisses et ordonnées sur un côté de
de cheminement polygonal dont les sommets sont connus en coordonnées (fig. 9.23).
